Hệ đếm là một tập các kí tự (bảng chữ số) để biểu diễn các số và xác định giá trị của các biểu diễn số.
Các hệ đếm thường gặp
Có 2 loại hệ đếm cơ bản mà chúng ta vẫn thường gặp là:
- Hệ đếm không vị trí (hệ la mã,... và trong bài viết này mình sẽ không nhắc tới)
- Hệ đếm có vị trí (hệ nhị phân, hệ thập phân, hệ thập lục phân,...)
1. Hệ số đếm có vị trí
Nguyên tắc chung
- Cơ số của hệ đếm r là số kí hiệu được dùng.
- Trọng số bất kì của một hệ đếm là ri (i có thể là số âm hoặc dương) giúp phân biệt giá trị biểu diễn của các chữ số khác nhau.
- Mỗi số được biểu diễn bằng một chuỗi các chữ số, trong đó số ở vị trí thứ i có trọng số ri
- Dạng tổng quát của một số trong hệ đếm có cơ số r là: (. . .a2a1a0.a-1a-2 . . .)r
- giá trị của chữ số ai là 1 số nguyên trong khoảng 0 < ai < r
Biểu diễn số tổng quát:
Khi biểu diễn số ta thường thêm chỉ số để nhận biết chính xác hệ cơ số đang xét, ví dụ: 1010, 102, 1016
2. Hệ thập phân
Hệ thập phân (hệ đếm cơ số 10) là hệ đếm dùng số 10 làm cơ số. Đây là hệ đếm được sử dụng rộng rãi nhất trong các nền văn minh thời hiện đại.
Hệ gồm các chữ số 0,1,2,3,4,5,6,7,8,9 tạo nên.
Ví dụ:
33 = (3*10) + 3
5432 = (5*1000) + (4*100) + (3*10) + 2
Cơ số 10. Tức là, mỗi chữ số trong số được nhân với 10 mũ i, i tương ứng với vị trí của chữ số đó:
3310 = 3*101 + 3*100
543210 = 5*103 + 4*101 + 3*101 + 2*100
Ví dụ biểu diễn số thực:
25.25610 = 2*101 + 5*100 + 2*10-1 + 5*10-2 + 6*10-3
- Chữ số ngoài cùng bên trái là chữ số quan trọng nhất
- Chữ số ngoài cùng bên phải là chữ số ít quan trọng nhất
- Lưu ý chữ số sau dấu '.' cũng được biểu diễn tương tự nhưng số mũ giảm dần từ -1
3. Hệ nhị phân
Hệ nhị phân (hay hệ đếm cơ số hai hoặc mã nhị phân) là một hệ đếm dùng hai ký tự để biểu đạt một giá trị số, bằng tổng các lũy thừa của 2.
- Hai chữ số: 0 và 1
- Cơ số 2
- Chữ số 1 và 0 trong ký hiệu nhị phân có cùng ý nghĩa như trong ký hiệu thập phân:
- 02 = 010
- 12 = 110
- Biểu diễn số nhị phân:
- Ví dụ:
- 102 = 1*21 + 0*20 = 210
- 1012 = 1*22 + 0*21 + 1*20 = 510
- 100.101 = 1*22 + 0*21 + 0*20 + 1*2-1 + 0*2-2 + 1*2-3 = 4.62510
- Lưu ý ở đây các hệ số bằng 0 chúng ta không cần viết vào cũng được
Cách chuyển đổi nhị phân sang thập phân:
Nhân mỗi chữ số nhị phân với 2i và cộng vào kết quả
Cách chuyển đổi từ thập phân sang nhị phân:
Đổi riêng phần nguyên và phần Thập phân
- Phần nguyên thập phân sang nhị phân:
- Cách 1:
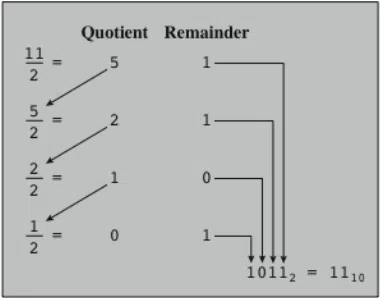
- Chia lặp đi lặp lại số đó cho 2. Phép chia dừng lại khi kết quả lần chia cuối cùng bằng 0.
- Lấy các số dư theo chiều đảo ngược sẽ được số nhị phân cần tìm.
- Cách 2:
- Phân tích số đó thành tổng của các số 2i
- Cách 1:
- Phần thập phân sang nhị phân:
- Nhân liên tiếp phần phân số của số thập phân với 2
- Lần lượt lấy phần nguyên của tích thu được sau mỗi lần nhân là kết quả cần tìm.
- Lấy phần phân số của tích nhân làm số bị nhân trong bước tiếp theo.
Ví dụ 1: Minh họa cách đổi 1110 sang nhị phân bằng cách 1
Ví dụ 2: Minh họa cách đổi 0.8110 sang nhị phân
Do 0.81 là một số vô tỉ nên ta không thể biết chính xác được số chữ số phía sau dấu '.' nên ở đây kết quả mình lấy 6 số sau dấu '.'
Ví dụ 3: Minh họa cách đổi 0.2510 sang nhị phân
Do 0.25 = 1/4 là một số hữu tỉ nên theo cách đổi trên ta hoàn toàn có thể xác định được chính xác số chữ số sau dấu '.' và 0.2510 = 0.012
Code C++ đổi phần nguyên từ thập phân sang nhị phân viết bằng đệ quy:
void DectoBin(int n)
{
if(n!=0)
{
DectoBin(n/2);
cout<<n%2;
}
}4. Hệ thập lục phân
Cơ số 16
Được tạo thành từ 16 chữ số bao gồm: 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
Biểu diễn thập lục phân:
- Không chỉ được dùng để biểu diễn các số nguyên mà còn là một biểu diễn ngắn gọn để biểu diễn dãy số nhị phân bất kỳ
- Lý do sử dụng biểu diễn thập lục phân:
- Ngắn gọn hơn ký hiệu nhị phân
- Trong hầu hết máy tính, dữ liệu nhị phân chiếm theo bội của 4 bit, tương đương với bội của một số thập lục phân duy nhất
- Rất dễ dàng chuyển đổi giữa nhị phân và thập lục phân
Cách chuyển từ nhị phân sang thập lục phân:
- Cách 1:
- Đổi từ hệ nhị phân sang thập phân, rồi từ hệ thập phân sang hệ thập lục phân như cách bên trên mình trình bày với hệ nhị phân (muốn từ nhị phân sang thập lục phân ta phải đổi trung gian qua hệ thập phân)
- Cách 2:
- Do mỗi chữ số của hệ thập lục phân được biểu diễn bằng 4 bit nhị phân, nên ta thường tính từ dấu '.' nhóm thành 4 bit một rồi chuyển từ nhị phân sang thập lục phân theo 4 bit đó qua cách mình tra bảng dưới đây:
Ví dụ 1: 100100112 = X16
Theo cách 2 thì mình chia thành 4 bit một từ phải qua trái là: 0011 và 1001 ở đây 1001 = 9 và 0011 = 3 => 100100112 = 9316
Ví dụ 2: 10011112 = X16
Theo cách 2 thì mình chia thành 4 bit một từ phải qua trái là: 1111 và 100, ta thấy ở đây 100 chỉ có 3 bit nên ta phải thêm cho nó 1 bit để đủ 4 bit và chúng ta thêm ở đâu cho đủ? Ở đây ta thêm 1 bit 0 vào bên phải để cho giá trị 0100 = 100 rồi ta tiếp tục tra bảng. 0100 = 4 và 1111 = F vậy 10011112 = 4F16
Ví dụ 3: 1100.1012 = X16
Do ví dụ này mình có thêm dấu '.' vào nên chúng ta phải đổi riêng phần nguyên và phần thập phân và cách đổi tương tự nhiên trên. Ta có phần nguyên là: 11002 = C16 và phần thập phân là 101, khi này ta cần nhớ lại chữ số ngoài cùng bên phải là chữ số ít quan trọng nhất vì vậy khi thêm 1 bit vào cho đủ 4 bit ta thêm bit 0 vào bên phải của 101 tức là 1010 = A. Vậy 1100.1012 = C.A16
Tổng kết lại ở cách đổi này ta cần lưu ý khi đổi phần nguyên ta nhóm 4 bit một từ phải qua trái tính từ dấu '.' khi thiếu bit ta thêm các bit vào bên trái cho đủ 4 bit rồi tra bảng. Khi đổi phần thập phân ta nhóm 4 bit một nhưng bây giờ ta nhóm từ trái qua phải tính từ dấu '.' và khi thiếu bit ta thêm các bit vào bên phải cho đủ 4 bit rồi tra bảng.
Tổng Kết
Qua bài viết trên mình đã trình bày cho các bạn cơ bản về các hệ số đếm như hệ nhị phân, hệ thập phân, hệ thập lục phân.
Mỗi phần mình đều liệt kê khái niệm, công thức tổng quát và cách đổi phần nguyên, phần thập phân.
Về cách đổi mình có trình bày cách đổi từ nhị phân sang thập phân, từ thập phân sang nhị phân, từ thập lục phân sang nhị phân bằng cách tra bảng.
Nói một cách tổng quát đổi cho tất cả hệ số nói chung: khi chuyển từ một hệ số bất kì qua hệ số 10 ta chỉ cần nhân với hệ số đó mũ i (ví dụ từ hệ 2 sang hệ 10 nhân 2^i, từ hệ 16 sang hệ 10 nhân 16^i,...) và khi chuyển từ hệ 10 sang các hệ số khác ta chia dư cho hệ đó (ví dụ từ hệ 10 sang hệ 2 ta chia 2, từ hệ 10 sang hệ 16 ta chia 16) Vậy nên khi chuyển từ hệ a sang b ta cần phải thông qua hệ số 10.
Tài liệu tham khảo: Computer Organization and Architecture, 9th Edition

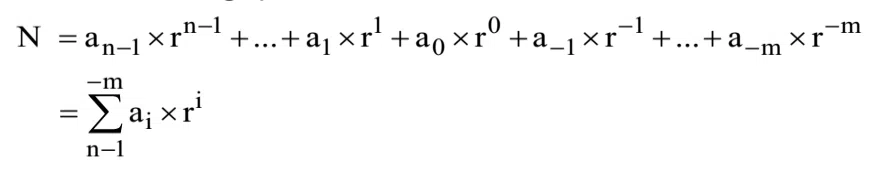
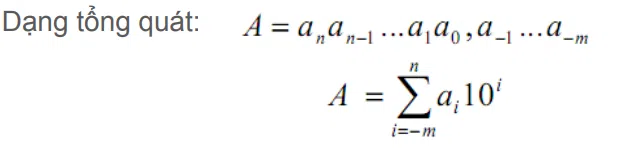
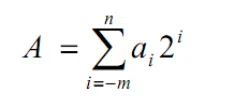



Bình luận