Khi nhìn các hình ảnh đồ thị trên bài giảng, sách báo, ta có thể ngay lập tức hiểu được chúng có những đỉnh nào, cạnh nào,… Vậy, làm thế nào để máy tính cũng có thể hiểu được những đồ thị đó có hình dạnh như thế nào?
Thông thường, sẽ có 3 cách sử dụng để biểu diễn đồ thị trên máy tính:
- Ma trận kề
- Danh sách cạnh
- Danh sách kề
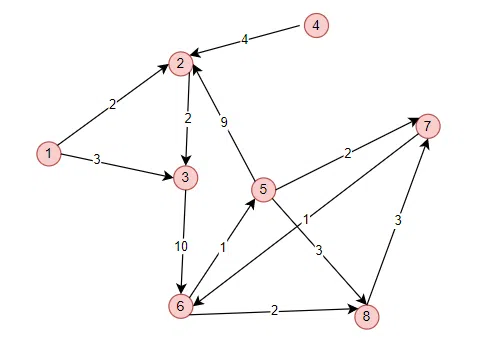
Cho một đồ thị như hình, ta sẽ cũng sử dụng ba cách trên để biểu diễn chúng dưới dạng máy tính có thể hiểu được.
Đồ thị G(V,E) trên có số đỉnh n=8 và số cạnh n=12
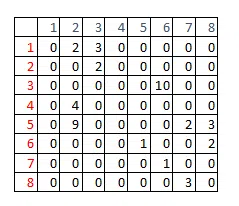
1. Ma trận kề Ta xây dựng một mảng 2 chiều A có kích thước n*n. Với mỗi cạnh e(u,v) = x đi từ đỉnh u tới đỉnh v, ta sẽ đặt giá trị A(u,v) là x. Ví dụ cạnh e(1,2) = 2 , ta sẽ gán A(1,2) = 2.Nhìn vào bảng, ta dễ dàng thấy được một cạnh và các đỉnh của đồ thị.
Các ưu điểm của ma trận kề
- Đơn giản, trực quan, dễ cài đặt
- Có thể kiểm tra một cạnh e(u,v) có tồn tại hay không bằng phép so sánh A(u,v) != 0
Các nhược điểm của ma trận kề
- Luôn phải dùng n^2 ô nhớ để lưu mảng A gồm n*n các phần tử
- Kiểm tra danh sách các đỉnh kề với đỉnh u bất kì, luôn cần duyệt từ n lần với phép toán A(u,v) != 0. Vì vậy, nếu muôn kiểm tra tổng số cạnh của đồ thị, cần phải duyệt cả bảng với độ phức tạp lên đến n^2
Danh sách cạnh
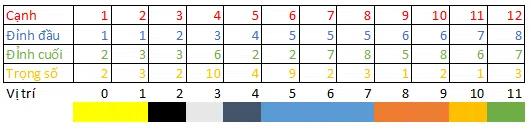
Cách biểu diễn của danh sách cạnh rất đơn giản, chỉ là một mảng hoặc danh sách các cạnh của đồ thị. Mỗi phần tử của mảng, cần lưu lại đỉnh đầu, đỉnh cuối và trọng số của cạnh đó.
Ta có thể ngay lập tức thấy được đồ thị có bao nhiêu cạnh và giá trị của chúng.
Các ưu điểm của danh sách cạnh
- Đơn giản, dễ cài đặt
- Tiết kiệm rất nhiều không gian lưu trữ trong trường hợp đồ thị thưa (chẳng hạn m < 6n)
- Dễ dàng duyệt các cạnh với các bài toán sử dụng đến tập hợp các cạnh như Kruskal.
Các nhược điểm của danh sách cạnh
- Nhược điểm cơ bản là khó tương tác với đỉnh. Chỉ riêng thao tác tìm danh sách các đỉnh kề với một đỉnh u, ta cũng phải duyệt hết cả danh sách cạnh.
Danh sách kề
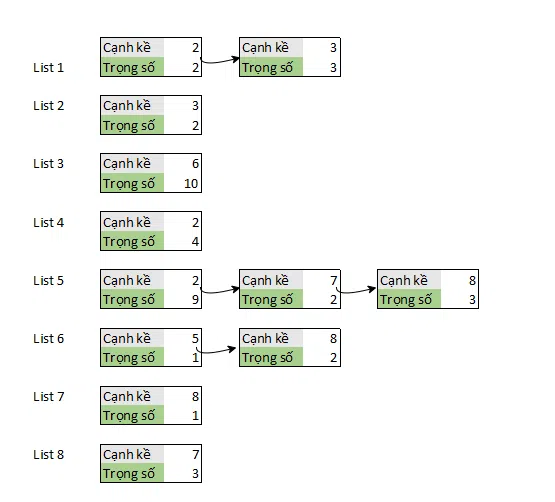
Để khắc phục một phần nhược điểm của ma trận kề cũng như danh sách cạnh, phương pháp danh sách kề được đề xuất. Cách biểu diễn của danh sách kề cũng tương tự như danh sách cạnh. Tuy nhiên,với mỗi đỉnh u của đồ thị, các cạnh kề với u sẽ được gộp vào một tập con với nhau.
Có 2 cách biểu diễn danh sách kề phổ biến. Với đồ thị của đề bài, ta sẽ biểu diễn chũng như sau:
- Chia mảng chứa danh sách cạnh làm n đoan nhỏ, mỗi đoạn thứ i là một tập các cạnh xuất phát từ đỉnh i. Lưu lại vị trí bắt đầu của đoạn.
Chia danh sách cạnh ra thành các đoạn.
Mảng Head lưu vị trí bắt đầu của các đoạn.
- Lưu n danh sách liên kết. Danh sách thứ i, lưu các cạnh xuất phát từ i.
- Lưu n danh sách liên kết. Danh sách thứ i, lưu các cạnh xuất phát từ i.
- Chia mảng chứa danh sách cạnh làm n đoan nhỏ, mỗi đoạn thứ i là một tập các cạnh xuất phát từ đỉnh i. Lưu lại vị trí bắt đầu của đoạn.
Các ưu điểm của danh sách kề
- Thao tác duyệt danh sách các cạnh tương tự như danh sách cạnh
- Tiết kiệm rất nhiều không gian lưu trữ hơn ma trận kề
- Cải tiến việc duyệt các cạnh kề đỉnh rất nhiều vì chỉ cần truy xuất tới đoạn từ Head[u] tới Head[u+1] với đỉnh u hoặc truy xuất trực tiếp vào List[u].
Các nhược điểm của danh sách kề
- Khó cài đặt hơn 2 phương pháp trên
- Yếu hơn ma trận kề khi kiểm tra một cạnh e[u,v] có tồn tại hay không
Kết luận:
Mỗi phương pháp biểu diễn đồ thị đều cho nhiều ưu và nhược điểm khác nhau, nên tùy theo không gian bài toán để quyết định nên chọn phương pháp biểu diễn nào là tối ưu hơn.
Chẳng hạn, khi nhập liệu một ma trận thưa chỉ có một vài cạnh, ta chọn nhập ma trận kề, sẽ rất tốn thời gian khi phải nhập n x n giá trị cho mảng trọng số.
Ngoài ra, cách cách biểu diễn có thể tùy biến cho nhau. Ví dụ, ta chọn nhập liệu đồ thị bằng danh sách cạnh, nhưng vẫn có thể lưu giá trị này vào ma trận kề.
Khởi tạo tất cả giá trị phần mảng A là 0
repeat
ReadLn(u, v, e); {Nhập một bộ (u, v), e là 2 đỉnh đầu cuối của 1 cạnh và trọng số}
if u <> 0:
A[u, v] = e; {gán giá trị cạnh vào ma trận kề}
until v = 0; {Nếu người sử dụng nhập giá trị i = 0 thì dừng quá trình nhập, nếu không thì tiếp tục}
Trong một số trường hợp, cũng phải để ý đến không gian lưu trữ của bài toán, nếu n là một số lớn, không nên sử dụng lưu trữ của ma trận kề. Bởi vì mà trận kề tốn n^2 vị trí nhớ cho tất cả các cạnh, gây lãng phí, hoặc thậm trí là không đủ bộ nhớ để lưu trữ.
Người sử dụng nên lưu ý là linh hoạt trong cách nhập liệu, lưu trữ và sử dụng các phương pháp biểu diễn ma trận này trong từng trường hợp để tối ưu hơn cho việc cài đặt cũng như dễ dàng hơn trong giải các bài toán về đồ thị.
Thân ái!



Bình luận