Có lẽ một trong những thuật toán nổi tiếng nhất từng có, nhưng vẫn còn rất nhiều người đấu tranh khi cố gắng tìm một giải pháp hiệu quả. Hãy để tôi giới thiệu bạn với chuỗi Fibonacci.
Xác Nhận
Cho một số N trả về giá trị chỉ số của dãy Fibonacci, trong đó trình tự là:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
Sau khi xem nhanh, bạn có thể dễ dàng nhận thấy rằng mẫu của chuỗi là mỗi giá trị là tổng của 2 giá trị trước đó, điều đó có nghĩa là đối với N = 5 → 2 + 3 hoặc trong toán học là:
F(n) = F(n-1) + F(n-2)
Triển khai đầu tiên
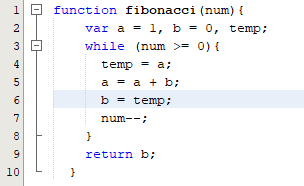
Trong lần triển khai đầu tiên ta dùng 1 vòng lặp đơn giản để đạt được giải pháp đó
Đây có lẻ là giải pháp đầu tiên bạn cần để tâm tới nó. Phần quan trọng ở đây là chúng tôi tính số tiếp theo bằng cách thêm số hiện tại vào số cũ. Độ phức tạp thuật toán là O(n). Khá tốt cho lần thử đầu tiên phải không? Nhưng hãy thử xem một số cách khác để tiếp cận vấn đề.
Giải pháp đệ quy
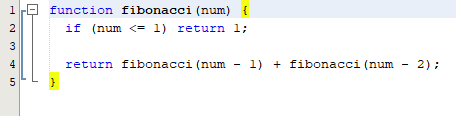
Bây giờ chúng ta hãy xem liệu chúng ta có thể làm cho nó trông ảo diệu hơn không, bây giờ chúng ta sẽ sử dụng đệ quy để làm điều đó.
Dễ dàng phải không? chúng ta vừa giải quyết được vấn đề trong 2 dòng code, nhưng hãy xem xét kỹ hơn và xem điều gì đang thực sự xảy ra.
Trường hợp cơ bản: chúng ta chỉ cần kiểm tra xem giá trị có nhỏ hơn 0 để trả về 2 trường hợp đầu tiên hay không.
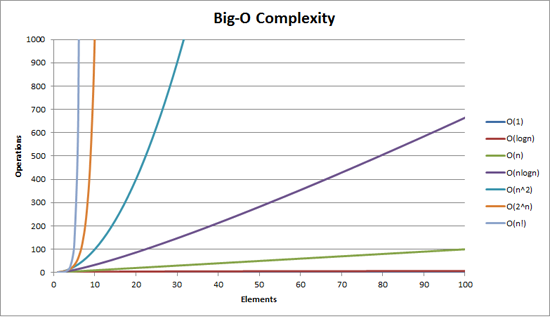
Nhưng bây giờ là tin xấu ... Chúng tôi đã tăng thời gian phức tạp của thuật toán của chúng tôi gần như đến trường hợp xấu nhất. Nếu bạn nhìn vào hình ảnh, bạn sẽ thấy sự phức tạp về thời gian màu cam (2 ^ N), có nghĩa là việc thực hiện hiện tại của chúng tôi là theo
Bản ghi nhớ
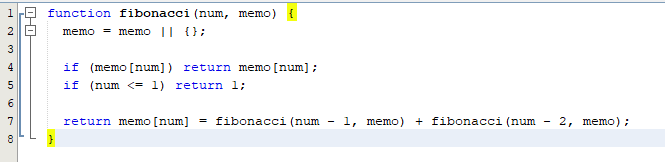
Cuối cùng, và theo cách tiếp cận đệ quy, chúng ta sẽ sử dụng tính năng ghi nhớ để cải thiện hiệu quả của chúng ta, nhưng trước hết, việc ghi nhớ là gì? như Wikipedia nói:
Là một kỹ thuật tối ưu hóa được sử dụng chủ yếu để tăng tốc các chương trình máy tính bằng cách lưu trữ các kết quả của các cuộc gọi hàm tốn kém.
Điều đó có nghĩa là gì và tại sao chúng ta nên quan tâm đến điều đó trong quá trình thực hiện? Về cơ bản, nếu chúng ta chỉ lưu trữ giá trị của mỗi chỉ mục trong một băm (hash), chúng ta sẽ tránh được thời gian tính toán của giá trị đó cho N lần tiếp theo.
Sự thay đổi này sẽ làm tăng độ phức tạp không gian của thuật toán mới của chúng ta thành O (n) nhưng sẽ làm giảm đáng kể độ phức tạp thời gian thành 2N, nó sẽ giải quyết thành thời gian tuyến tính vì 2 là hằng số.
Điểm chuẩn
Hãy sử dụng 50 làm số đầu vào và xem nó như thế nào:
Vòng lặp While
Độ phức tạp thời gian: O (N)
Độ phức tạp của không gian: Hằng số
Lời gọi hàm: 51
Thời gian cần thiết: 0.000001ms
Đệ quy
Độ phức tạp thời gian: O (2 ^ N)
Độ phức tạp của không gian: O (n)
Lời gọi hàm: 20.365.011.074
Thời gian cần thiết: 176.742ms
Memoization
Độ phức tạp thời gian: O (2N)
Độ phức tạp của không gian: O (n)
Lời gọi hàm: 99
Thời gian cần thiết: 0.000001ms
Kết quả Jsperf
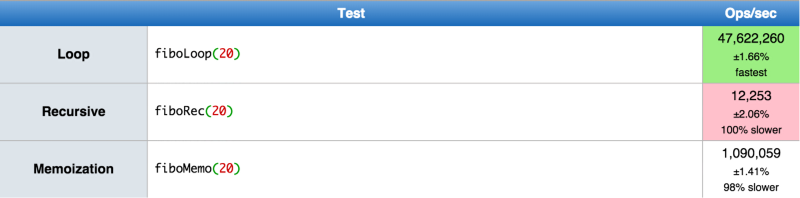
Tôi cũng tạo bản trình diễn jsPerf demo với 3 trường hợp, Bạn có thể nhìn dưới đây:
Phần kết luận
Đây chỉ là một ví dụ về cách thiết kế, cải tiến và phân tích một thuật toán, trong trường hợp này nó là dãy Fibonacci, đủ đơn giản để hiểu và ngạc nhiên khi thấy hiệu suất mà chúng ta đạt được chỉ với một số thay đổi nhỏ.
Bài viết được dịch từ trang: https://medium.com

Bình luận