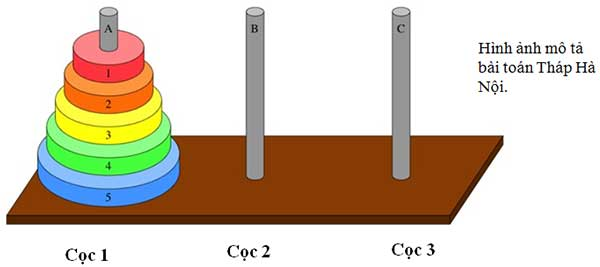
Bài toán tháp Hà nội giải bằng đệ quy

Bài toán

Tháp Hà Nội là một bài toán kinh điển có thể giải bằng đệ quy. Đó là một câu đố bao gồm ba cọc và một số đĩa có kích thước khác nhau, có thể đặt lên bất kỳ cọc nào. Câu đố bắt đầu với các đĩa xếp thành chồng theo thứ tự kích thước tăng dần trên một cọc, nhỏ nhất ở trên cùng, do đó tạo thành hình nón.

Mục tiêu của câu đố là di chuyển toàn bộ đĩa sang một cọc khác, tuân theo quy tắc đơn giản sau:

• Mỗi lần chỉ có thể di chuyển một đĩa.
• Mỗi lần di chuyển : lấy đĩa từ một cọc nguồn và đặt nó lên một cọc đích. Ở cọc đích có thể đã có sẵn các đĩa.
• Không có đĩa nào có thể được đặt trên một đĩa nhỏ hơn.
• Có thể chuyển đĩa vào cọc trung gian miễn là tuân thủ 3 quy tắc trên.
  

Giải bằng cơm trước khi code

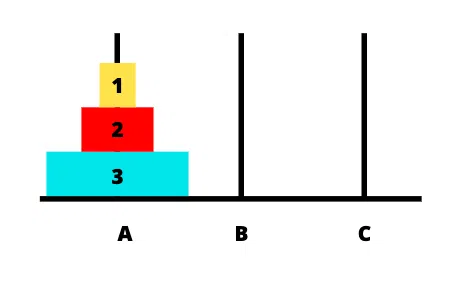
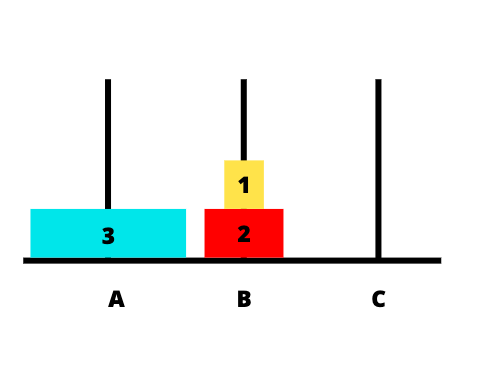
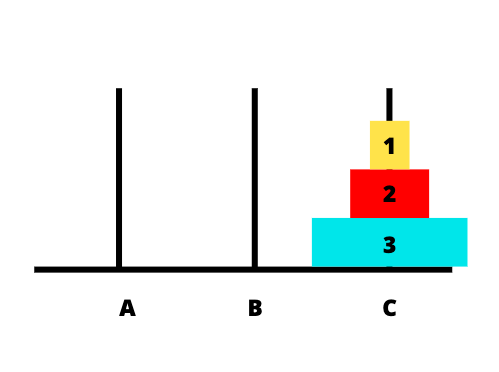
Để dễ hình dung hơn các bước giải, chúng ta sẽ lấy ví dụ cụ thể. Giả sử chúng ta có 3 cọc A, B, C tương trưng cho 3 tháp và có 3 đĩa.
Ảnh dưới là trạng trái ban đầu

Để đưa toàn bộ 3 đĩa ở cọc A tới cọc C, bạn cần:

• Chuyển đĩa 1 và 2 sang cọc trung gian B.
• Di chuyển đĩa 3 sang cọc C
• Chuyển đĩa 1 và 2 sang cọc C

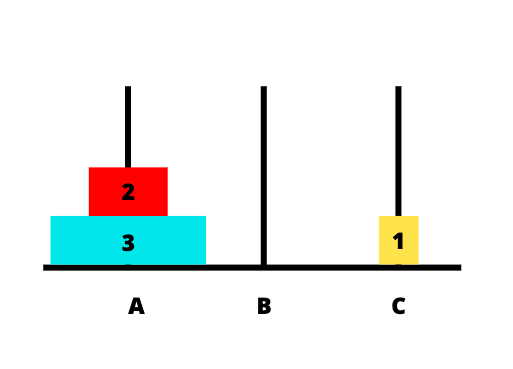
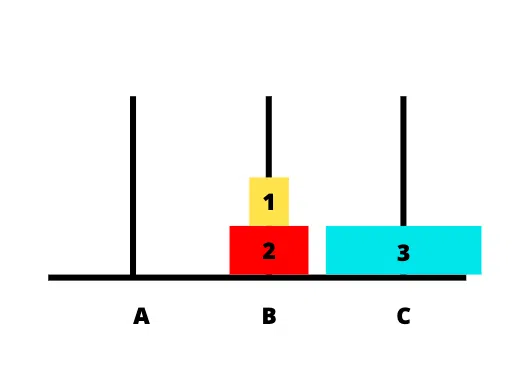
Bước 1: chuyển đĩa 1 từ cọc A sang cọc C

Bước 2: chuyển đĩa 2 từ cọc A sang cọc B

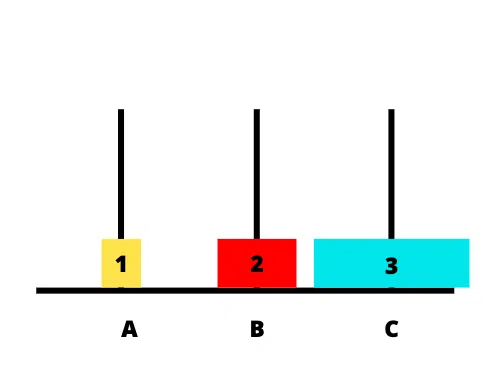
Bước 3: chuyển đĩa 1 từ cọc C sang cọc B

Mục đích bước này để dành chỗ ở cọc C chuyển đĩa 3 từ cọc A sang

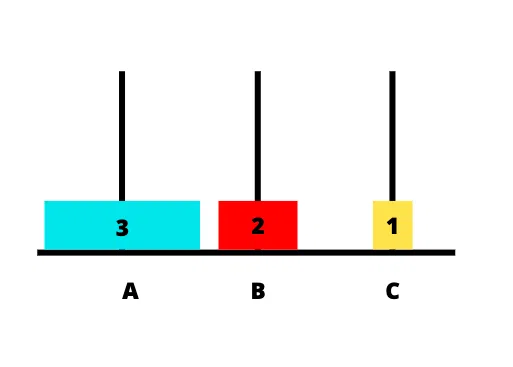
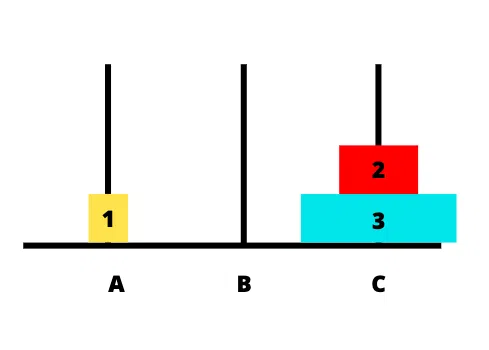
Bước 4: chuyển đĩa 3 từ cọc A sang cọc C

Bước 5: chuyển đĩa 1 từ cọc B sang cọc A

Bước 6: chuyển đĩa 2 từ cọc B sang cọc C

Bước 7: chuyển đĩa 1 từ cọc A sang cọc C

Đến bước này ta đã hoàn thành nhiệm vụ

Thuật toán đệ quy

• Di chuyển n-1 đĩa trên cùng từ cọc nguồn sang cọc trung gian.
• Di chuyển đĩa thứ n từ cọc nguồn đến cọc đích.
• Di chuyển n-1 đĩa từ cọc trung gian sang cọc đích, sử dụng cọc nguồn làm trung gian.
• Trường hợp cơ bản của đệ quy là khi chỉ có một đĩa để di chuyển. Trong trường hợp này, chúng ta chỉ cần di chuyển đĩa từ cọc nguồn đến cọc đích.

public class HanoiTower {
    public static void solveHanoi(int n, char source, char destination, char auxiliary) {
        if (n == 1) {
            System.out.println("Move disk 1 from " + source + " to " + destination);
            return;
        }
        solveHanoi(n-1, source, auxiliary, destination);
        System.out.println("Move disk " + n + " from " + source + " to " + destination);
        solveHanoi(n-1, auxiliary, destination, source);
    }

    public static void main(String[] args) {
        int n = 3;
        solveHanoi(n, 'A', 'C', 'B');
    }
}
java

Có thể viết dưới dạng hàm trong unit test bằng JUnit5

package leetcode;
import org.junit.jupiter.api.Test;
public class HanoiTower {
  public static void solveHanoi(int n, char source, char destination, char auxiliary) {
    if (n == 1) {
      System.out.println("Move disk 1 from " + source + " to " + destination);
      return;
    }
    solveHanoi(n - 1, source, auxiliary, destination);
    System.out.println("Move disk " + n + " from " + source + " to " + destination);
    solveHanoi(n - 1, auxiliary, destination, source);
  }

  @Test void test() {
    int n = 3;
    solveHanoi(n, 'A', 'C', 'B');
  }
}
java

Kết quả in ra màn hình các bước

Move disk 1 from A to C
Move disk 2 from A to B
Move disk 1 from C to B
Move disk 3 from A to C
Move disk 1 from B to A
Move disk 2 from B to C
Move disk 1 from A to C