Các bạn có thể xem miễn phí nội dung cuốn sách tại địa chỉ: https://use-the-index-luke.com/

Chào mừng các bạn đến với series bài viết: Biên dịch sách "SQL Performance Explained" của tác giả Markus Winand

Trong series này, với mỗi bài viết tôi sẽ biên dịch lại nội dung của một chương trong cuốn sách

  • Cuốn sách này gồm 9 chương:
  1.  Anatomy of an Index
  2. The Where Clause
  3. Performance and Scalability
  4. The Join Operation
  5. Clustering Data
  6. Sorting and Grouping
  7. Partial Results
  8. Modifying Data
  9. Execution Plans

 

Chương 1: Anatomy of an Index

Với index, câu cửa miệng của mọi developer sẽ là: Index giúp query dữ liệu nhanh hơn. Đúng, nhưng chưa đủ. Cuốn sách này sẽ giúp bạn đi xa hơn thế

Một index là một cấu trúc dữ liệu riêng biệt trong database. Nó sở hữu một vùng nhớ riêng trong disk. Nó lưu một bản copy của dữ liệu được đánh index. Việc tạo một index không gây ảnh hưởng gì đến dữ liệu trong bảng

Việc tìm kiếm dữ liệu bên trong 1 index diễn ra rất nhanh vì dữ liệu đã được sắp xếp theo thứ tự

Khi các lệnh INSERT, DELETE, UPDATE được thực hiện, bên cạnh việc thay đổi dữ liệu trong bảng, database còn phải thay đổi dữ liệu trong index sao cho dữ liệu vẫn phải được sắp xếp theo đúng thứ tự. Để thực hiện việc này, database sử dụng 2 kiểu cấu trúc dữ liệu: Doubly Linked List và Tree

Index không lưu dữ liệu theo cách tuần tự: Khi lưu dữ liệu theo cách này, mỗi khi INSERT một bản ghi, để đảm bảo index được sắp xếp đúng thứ tự thì database sẽ phải dịch chuyển các bản ghi có giá trị lớn hơn bản ghi được INSERT vào, khiến cho việc INSERT mất nhiều thời gian. Để giải quyết vấn đề này, database sẽ thiết lập một "trật tự logic" độc lập với vị trí của dữ liệu trong bộ nhớ

Để duy trì "trật tự logic" này, database sẽ sử dụng cấu trúc dữ liệu Doubly Linked List: Với cấu trúc này, mỗi một node sẽ có 2 con trỏ: 1 con trỏ hướng đến node liền trước, 1 con trỏ hướng đến node liền sau. Mỗi khi có dữ liệu mới được INSERT vào, database sẽ thực hiện 2 việc hoàn toàn độc lập nhau là lưu bản ghi mới vào ô nhớ và duy trì trật tự logic: một node mới được tạo ra, 2 node liền trước và liền sau node mới này chỉ cần cập nhật lại vị trí con trỏ là được.

Database dùng Doubly Linked List để kết nối các index leaf nodes. Mỗi một index leaf nodes sẽ được lưu trong một database block, trong mỗi block sẽ có nhiều dữ liệu của cột được đánh index (index entry). Điều này có nghĩa index duy trì trật tự của nó ở 2 mức: giữa các index entry trong cùng 1 block và giữa các block với nhau

Ảnh 1.1: Index leaf nodes và dữ liệu tương ứng trong bảng
Ảnh 1.1: Index leaf nodes và dữ liệu tương ứng trong bảng

Trong ảnh 1.1, mỗi index entry gồm 2 thành phần: Dữ liệu của cột được đánh index (cột số 2) và một con trỏ ROW_ID trỏ đến vị trí của bản ghi chứa dữ liệu của cột được đánh index (cột số 2). Lưu ý: Dữ liệu trong bảng được lưu trong 1 cấu trúc dạng heap và không được sắp xếp. Không có bất kì mối liên hệ nào giữa các bản ghi trong 1 table block hay giữa các table blocks với nhau

Các index leaf nodes được săp xếp theo trật tự "logic", nghĩa là vị trí của một bản ghi trên disk rất có thể không khớp với vị trí của bản ghi đó nếu chiếu theo trật tự của index leaf nodes. Giống như khi bạn mở 1 cuốn danh bạ điện thoại để tìm số điện thoại của Ronaldo nhưng khi bạn mở trang đầu tiên thì cái tên đầu tiên đập vào mắt bạn là Messi, tức là chẳng có gì đảm bảo rằng Ronaldo sẽ là cái tên tiếp theo (biết đâu tên tiếp theo lại là Buffon ?). Vì thế, database cần sử dụng một kiểu cấu trúc dữ liệu khác nữa để tìm kiếm nhanh: balanced search tree (B-Tree)

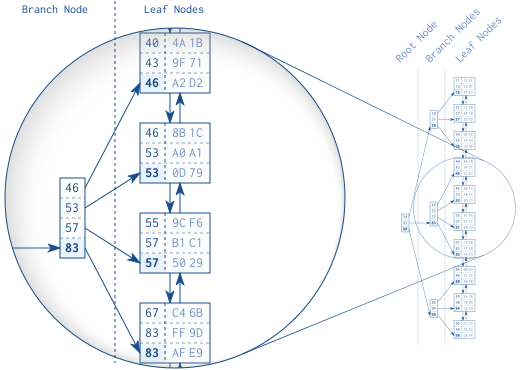
Ảnh 1.2: Cấu trúc B-Tree với Root/Branch/Leaf Nodes
Ảnh 1.2: Cấu trúc B-Tree với Root/Branch/Leaf Nodes

Ảnh 1.2 minh họa một cấu trúc index với 30 entries. Cấu trúc Doubly Linked List thiết lập một trật tự logic giữa các index leaf nodes. Còn các root và branch node hỗ trợ tìm kiếm nhanh giữa một rừng các leaf node. Trong cấu trúc này, mỗi một branch node sẽ trỏ đến một index entry có giá trị lớn nhất trong một leaf node. Như trong ảnh 1.2, trong một branch node với các giá trị [46,53,57,83], giá trị đầu tiên: 46 sẽ là giá trị lớn nhất của một index leaf node gồm các giá trị [40, 43, 46]. Tương tự, 53 là giá trị lớn nhất của index leaf node gồm [46, 53, 53], ...

Các branch node tiếp theo được xây dựng tương tự, lớp sau được tạo nên bởi các giá trị lớn nhất của lớp trước. Quy trình này được lặp lại cho đến khi chỉ còn 1 node duy nhất, gọi là root node. Cấu trúc này được gọi là "Cây tìm kiếm cân bằng" (Balanced Search Tree), "cân bằng" bởi vì khoảng cách từ root node đến một leaf node bất kỳ là như nhau

Sau mỗi một lệnh INSERT/UPDATE/DELETE, database sẽ tự động cập nhật Balanced Search Tree, giữ cho nó luôn cân bằng. Điều này sẽ khiến cho các câu lệnh INSERT/UPDATE/DELETE trở nên chậm hơn. Vấn đề này sẽ được giải thích rõ hơn trong Chapter 8: Modifying Data

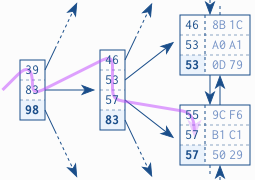
Ảnh 1.3: Tìm kiếm giá trị 57 trong Balanced Search Tree
Ảnh 1.3: Tìm kiếm giá trị 57 trong Balanced Search Tree

Ảnh 1.3 minh họa quá trình tìm kiếm một index entry có giá trị 57. Quy trình như sau:

  • Bắt đầu từ root node với 3 giá trị: 39, 83, 98
  • So sánh 57 với giá trị đầu tiên là 39: 57 > 39, trong khi 39 là giá trị lớn nhất của branch node mà 39 trỏ đến --> 57 sẽ không nằm trong branch node đó
  • So sánh 57 với giá trị thứ hai là 83: 57 < 83 --> 57 rất có thể nằm trong branch node mà 83 trỏ đến --> bắt đầu tìm kiếm trong branch node này
  • Quy trình tìm kiếm lại tiếp tục tại branch node mà root node 83 trỏ đến, gồm các giá trị: 46, 53, 57, 83
  • So sánh 57 với giá trị đầu tiên là 46: 57 > 46 --> 57 không nằm trong leaf node mà 46 trỏ đến
  • Tương tự, 57 > 53 --> 57 không nằm trong leaf node mà 53 trỏ đến
  • 57 <= 57 --> 57 sẽ nằm trong leaf node mà 57 (giá trị ở branch node) trỏ đến
  • Quy trình tìm kiếm lại lặp lại tại leaf node gồm các giá trị: 55, 57, 57
  • 57 > 55 --> không phải giá trị cần tìm --> tìm tiếp
  • 57 = 57 --> Eureka !!! đây chính là giá trị cần tìm, nhưng quá trình tìm kiếm vẫn tiếp tục, vì biết đầu giá trị tiếp theo trong leaf node cũng là 57
  • 57 = 57 --> Hoorayy !!! Lại tìm thêm được một giá trị 57 nữa
  • Tất các các giá trị trong leaf node đều đã được check, quá trình tìm kiếm kết thúc. Kết quả thu được là 2 giá trị 57 ứng với 2 ROW_ID trỏ đến 2 bản ghi trong database

Quá trình tìm kiếm trên được gọi là tree traversal - tìm kiếm dọc theo cây.Tree traversal đặc biệt hiệu quả vì 2 nguyên nhân:

  • Thứ nhất: mọi phần tử trong leaf node đều có thể được tìm ra trong cùng 1 số lượng bước nhất định
  • Thứ hai: Độ sâu của cây (tree depth) tăng rất chậm so với tốc độ tăng của số lượng leaf nodes.

Hết phần 1