Tác giả: Lê Trung Kiên lớp java 08
Email: lekien.2803.cg@gmail.com
SĐT: 0942096947
Link bài toán: https://leetcode.com/problems/sum-multiples/
1. Mở đầu
Xin chào các bạn, mình viết ra bài viết này để chia sẻ phương pháp giải cũng như tư duy của mình về bài toán này của leetcode. Phương pháp của mình có thể không phải là tối ưu nhất, tuy nhiên mình sẽ phân tích, chia nhỏ bài toán ra thành các module nhỏ hơn để dễ giải quyết cũng như giúp các bạn hiểu được các yêu cầu mà bài toán đưa ra.
2. Đề bài
Cho một số nguyên dương n, tìm tổng của tất cả các số trong khoảng [1, n] mà chia hết cho 3, 5 hoặc 7.
Trả về kết quả là tổng của các số thỏa mãn điều kiện.
Điều kiện:
1 <= n <= 103.
Ví dụ 1:
Input: n = 7
Output: 21
Explanation: Numbers in the range [1, 7] that are divisible by 3, 5, or 7 are 3, 5, 6, 7. The sum of these numbers is 21.
Ví dụ 2:
Input: n = 10
Output: 40
Explanation: Numbers in the range [1, 10] that are divisible by 3, 5, or 7 are 3, 5, 6, 7, 9, 10. The sum of these numbers is 40.
Ví dụ 3:
Input: n = 9
Output: 30
Explanation: Numbers in the range [1, 9] that are divisible by 3, 5, or 7 are 3, 5, 6, 7, 9. The sum of these numbers is 30.
3. Phân tích
Âu kê, một bài tập dạng cơ bản. Trong khoảng các số từ [1, n] ta cần tìm ra các số chia hết hoặc là chia hết cho 3 hoặc 5 hoặc 7. Tìm được rồi thì cộng hết lại với nhau rồi trả về kết quả là xong.
Với bài này tôi có hai cách để giải quyết:
Cách 1: Sử dụng thuật toán Brute Force (thuật toán vét cạn)
Với cách này, chúng ta chỉ đơn giản là dùng một vòng lặp với con trỏibắt đầu từ số3luôn, không phải bắt đầu1vì1và2chắc chắn không chia hết cho3rồi. Đặt điều kiện kiểm tra xem số nào chia hết cho một trong ba số trên, nếu thỏa mãn điều kiện thì cộng dồn vào luôn. Sau đó thì trả về kết quả là được.
Đây là cách làm cơ bản, miễn là chúng ta giải ra được kết quả là ok. Tuy nhiên nhược điểm của cách làm này là chúng ta sẽ phải kiểm tra từng số, thậm chí phải kiểm tra cả những số không thỏa mãn điều kiện, như vậy hơi mất thời gian. Vậy nên hãy đến với cách thứ hai, hơi hướng toán học một chút.Cách 2:
Để tính tổng các số hoặc chia hết cho3hoặc5hoặc7, ta sẽ tách ra tính tổng các số chia hết cho3,5và7riêng rồi cộng chúng lại. Và kiến thức chúng ta sử dụng ở đây là Cấp số cộng (Toán lớp 11).
Hãy lấy ví dụn = 12thì các số chia hết cho3sẽ là dãy số: 3, 6, 9, 12. Dãy số này cách nhau 3 đơn vị, cũng chính là công sai của dãy số này. Ta có công thức:Trong đó:
- d là công sai, cụ thể ở đây là
3(nếu tìm các số chia hết cho5thì sẽ bằng5, tương tự với7). - n là số hạng cuối cùng trong dãy số chia hết cho
d.
Ok, sau khi tìm được tổng các số chia hết cho (CHC)
3,5và7rồi thì ta cộng chúng vào với nhau. Tuy nhiên có một vấn đề, ấy là sẽ có những số cùng CHC cả3và5, cả5và7, cả7và3trùng nhau trong cái tổng ta áp dụng công thức kia. Ví dụn = 35thì ta sẽ có15cùng CHC3và5;21cùng CHC3và7;35thì CHC cho7và5. Vậy thì ta sẽ phải trừ đi những cái số này nếu không sẽ bị trùng. Nhưng mà lại xảy một vấn đề nữa ấy là riêng những số CHC cả ba số3,5,7(cụ thể là những số CHC105) thì vô tình bị trừ đi rồi, vậy nên ta phải cộng lại.
Nghe rắc rối nhỉ, nhưng đừng lo, hãy thử xem code chạy như thế nào nhé.- d là công sai, cụ thể ở đây là
4. Code chạy bằng cơm
Ta sẽ tạo ra riêng một function làm nhiêm vụ tính tổng các số chia hết cho một số, với đầu vào sẽ là số n ban đầu, cùng với các số 3, 5, 7 là công sai.
Trước hết ta phải tìm ra số hạng cuối cùng trong dãy số có thể chia hết cho d (công sai). Bằng cách lấy n/d ta sẽ có được số hạng cuối. Hãy thử với ví dụ n = 15 và d = 3:
Áp dụng công thức Cấp số cộng ở trên ta có tổng các số CHC 3 sẽ là:
Tương tự với các số CHC 5:
Với các số CHC 7 cũng vậy:
Ok, như đã nói ở trên, sẽ có những số cùng chia hết cho một trong các cặp số 3, 5 và 7. Ta sẽ làm trừ đi những tổng các số CHC các cặp số ấy, cụ thể trong ví dụ này có 15 cùng CHC 3 và 5. Trước hết ta sẽ tính tổng của các số CHC 15 đã:
Ta cộng ba cái tổng các số CHC riêng cho 3, 5, 7 rồi trừ đi tổng CHC cho 15:
Các bạn sư dụng cách 1 cũng sẽ ra kết quả tương tự.
5. Code chạy bằng máy
5.1. Sử dụng thuật toán Brute Force
Code cua chúng ta như sau:
public static int sumOfMultiples(int n) {
int sum = 0;
int i = 3;
while (i <= n) {
if (i % 3 == 0 || i % 5 == 0 || i % 7 == 0) {
sum += i;
}
i++;
}
return sum;
}
5.2. Sử dụng công thức Cấp số cộng
Code của chúng ta sẽ như sau:
public static int sumOfMultiples1(int n){
int CHC3 = tinhTong(n, 3);
int CHC5 = tinhTong(n, 5);
int CHC7 = tinhTong(n, 7);
int CHC3va5 = tinhTong(n, 15);
int CHC5va7 = tinhTong(n, 35);
int CHC3va7 = tinhTong(n, 21);
int CHC3va5va7 = tinhTong(n, 105);
return CHC3 + CHC5 + CHC7 - CHC3va5 - CHC5va7 - CHC3va7 + CHC3va5va7;
}
public static int tinhTong(int num, int d){
int n = num/d;
return d * n * (n + 1) / 2;
}
6. Kết thúc
Qua bài viết này, mình đã chia sẻ cho các bạn cách mình tư duy khi giải bài tập trên leetcode. Hi vọng bài viết giúp ích cho các bạn trong cách tư duy để giải các bài tập khác. Xin cám ơn các bạn đã dành thời gian đọc và theo dõi. Peace!!!

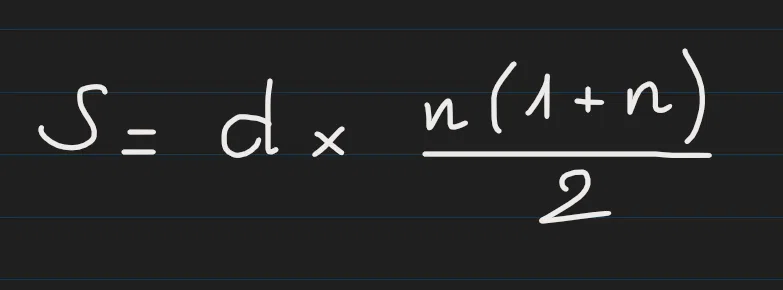

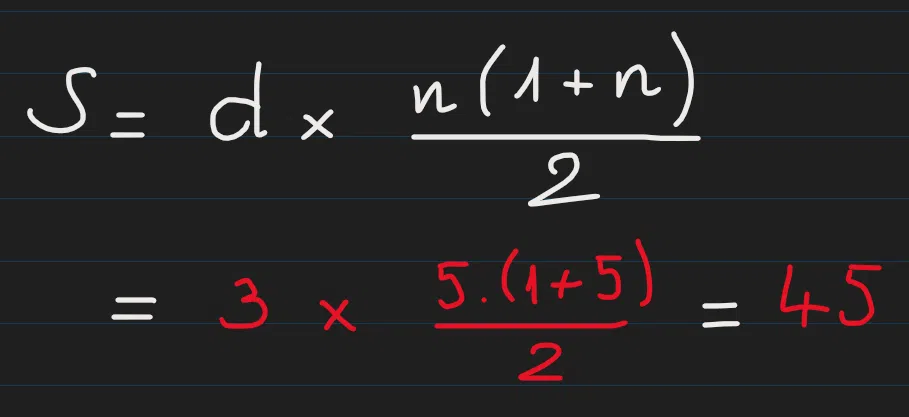
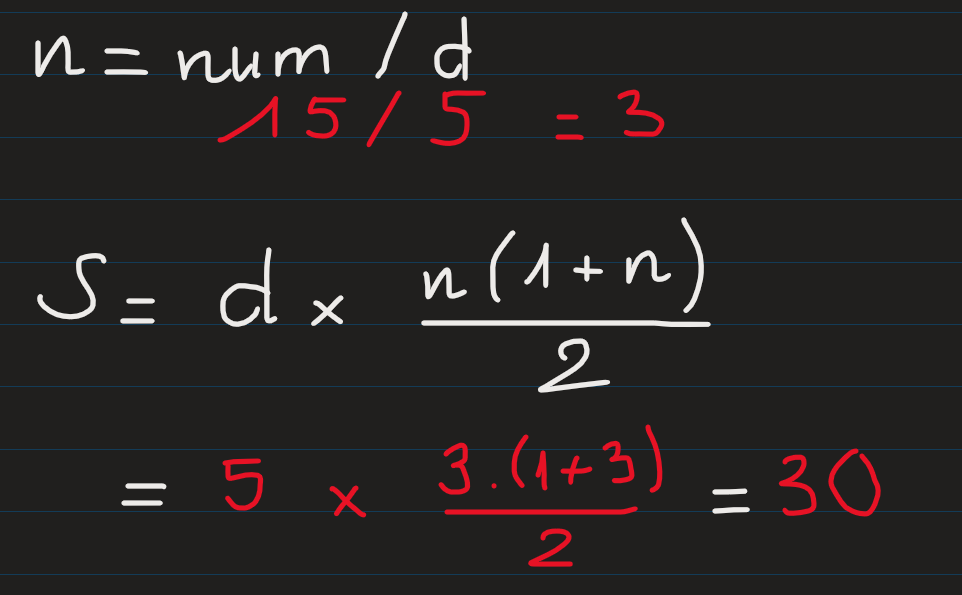
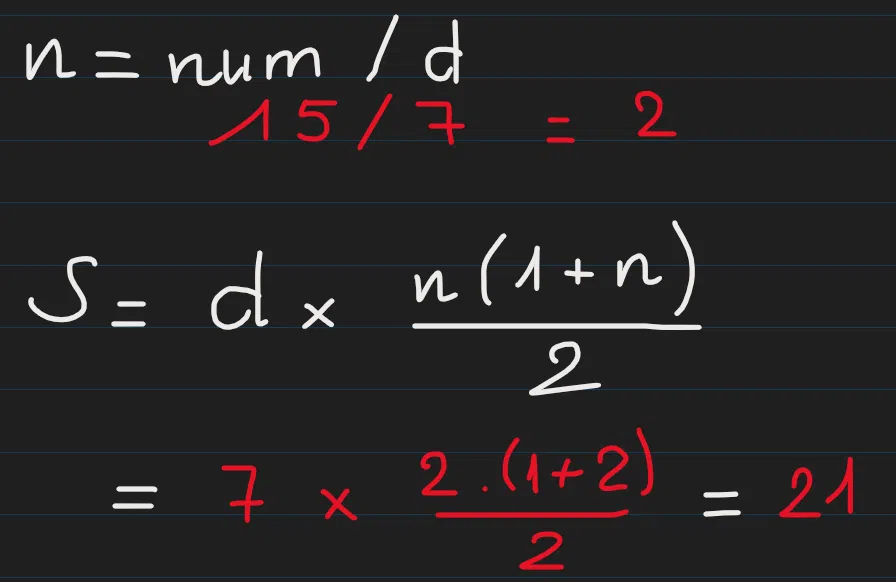
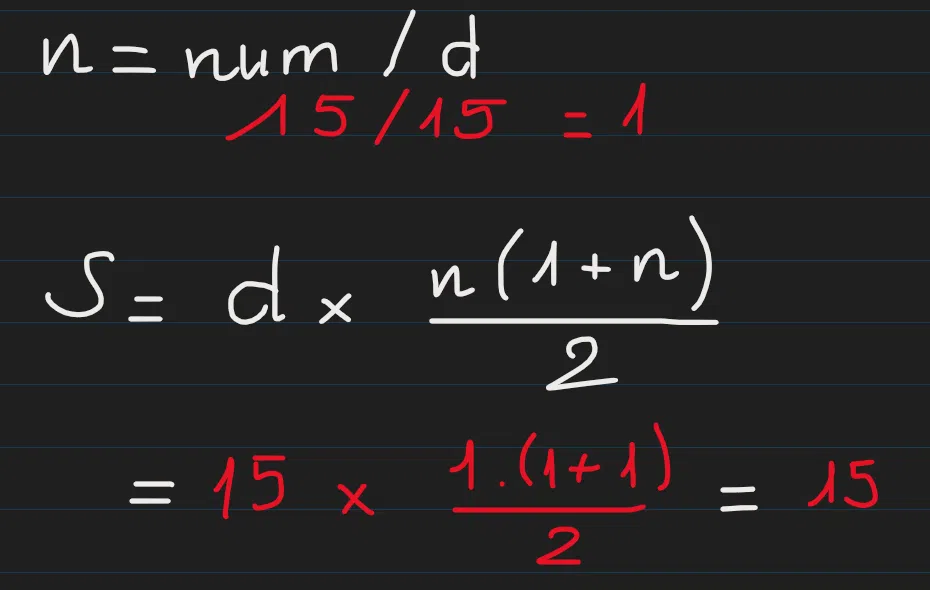
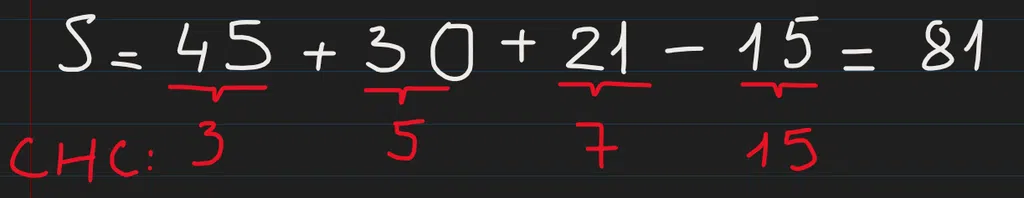
Bình luận