Tác giả: Lê Trung Kiên lớp java 08
Email: lekien.2803.cg@gmail.com
SĐT: 0942096947
Link bài toán: https://leetcode.com/problems/binary-search/
1. Mở đầu
Xin chào các bạn, mình viết ra bài viết này để chia sẻ phương pháp giải cũng như tư duy của mình về bài toán này của leetcode. Phương pháp của mình có thể không phải là tối ưu nhất, tuy nhiên mình sẽ phân tích, chia nhỏ bài toán ra thành các module nhỏ hơn để dễ giải quyết cũng như giúp các bạn hiểu được các yêu cầu mà bài toán đưa ra.
2. Đề bài
Cho một mảng số nguyên nums sắp xếp theo thứ tự tăng dần và một số nguyên target. Hãy tìm số nguyên target trong mảng nums rồi trả về index của target, nếu không tìm thấy thì trả về -1.
Bạn phải viết một thuật toán với độ phức tạp thời gian chạy O(log n).
Điều kiện:
1 <= nums.length <= 104.-104 < nums[i], target < 104.- Tất cả số nguyên trong mảng
numskhông trùng lặp. numssắp xếp theo thứ tự tăng dần.
Ví dụ 1:
Input: nums = [-1,0,3,5,9,12], target = 9
Output: 4
Explanation: 9 exists in nums and its index is 4
Ví dụ 2:
Input: nums = [-1,0,3,5,9,12], target = 2
Output: -1
Explanation: 2 does not exist in nums so return -1
3. Phân tích
Bình thường là chúng ta có thể sử dụng thuật toán Brute Force (thuật toán vét cạn) đấy. Với một vòng lặp for duyệt từ đầu tới cuối mảng, và điều kiện nums[i] = target thì ta trả về i là xong. Tuy nhiên, đề bài họ yêu cầu chúng ta viết một function với độ phức tạp theo thời gian là O(log n), vậy nên chúng ta sẽ giải quyết bài toán này với thuật toán đệ quy, hay cụ thể hơn chúng ta sẽ sử dụng thuật toán Binary Search (Tìm kiếm nhị phân). Điều kiện của thuật toán này là sử dụng với một mảng đã được sắp xếp theo thứ tự.
Chúng ta sẽ làm các bước sau:
Bước 1: Tìm ra số nằm chính giữa mảng
nums, bằng cách lấy tổng của index bên trái với index bên phải chia cho2.Bước 2: Ta so sánh số đó với
target, nếu bằng nhau thì ta trả về index của số đó. Nếu nó nhỏ hơntarget, nghĩa là số cần tìm nằm ở bên phải của số chính giữa, ta lặp lại Bước 1 ở trên, nhưng lúc này index bên trái lại bằng index chính giữa cộng với1. Nếu số chính giữa lớn hơntarget, nghĩa là số cần tìm nằm phía bên trái của số chính giữa, ta lặp lại Bước 1, nhưng khi này index bên phải sẽ là index chính giữa trừ đi1.Bước 3: Ta sẽ lặp đi lặp lại công việc trên đến khi tìm ra được số cần tìm. Tuy nhiên, nếu số index trái mà lớn hơn index phải, nghĩa là số cần tìm không tồn tại trong mảng
nums, chúng ta sẽ trả về kết quả-1.Cụ thể hơn chúng ta sẽ sang bước tiếp theo để xem nó hoạt động như thế nào nhé!
4. Code chạy bằng cơm trước
4.1. Ví dụ 1
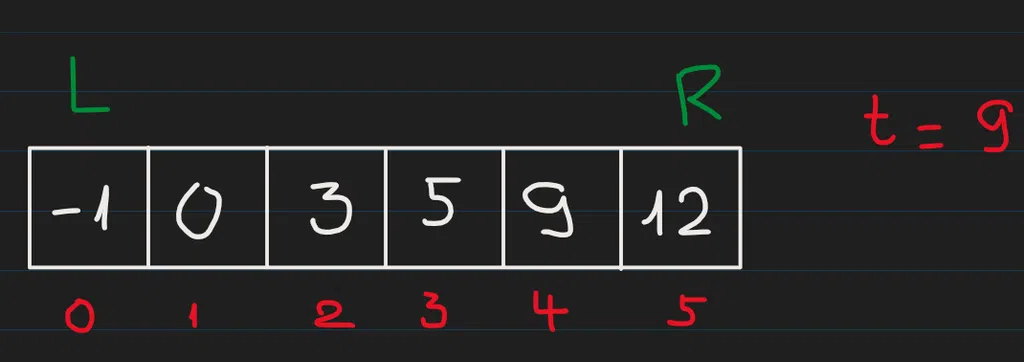
Ok. Hãy thử luôn vào ví dụ 1 ở trên. Chúng ta có mảng nums = [-1,0,3,5,9,12] và target = 9. Đầu tiên thì index bên trái và phải ta sẽ tạm gọi là L và R sẽ có giá trị là tận cùng hai đầu của mảng, hay nói cách khác L = 0 và R = n - 1 = 5.
Tiếp theo, để tìm index chính giữa, tạm gọi là mid ta sẽ lấy (L + R) / 2:
Khi này ta so sánh nums[mid] với target thì thấy 3 < 9 nên suy ra số cần tìm nằm phía bên phải của mid:
Ta lặp lại bước đầu tiên, nhưng lần này L = mid + 1. Ta lại tìm mid:
Lúc này ta so sánh nums[mid] thì thấy bằng với target, thỏa mãn điều kiện đề bài, ta trả về kết quả là mid chính là index của target trong mảng nums:
4.2. Ví dụ 2
Hãy thử với ví dụ 2 với nums = [-1,0,3,5,9,12] và target = 2. Chúng ta sẽ tìm mid trước:
Sau đó ta so sánh nums[mid] với target thì thấy 3 > 2 nên số cần tìm nằm ở phía bên trái của mid:
Ta lặp lại bước trên, tuy nhiên thì lúc này R = mid - 1:
So sánh nums[mid] với target thì thấy -1 < 2 nên số cần tìm nằm ở phía bên phải của mid:
Ta lặp lại bước tìm mid với L = mid + 1:
So sánh nums[mid] với target thì thấy 0 < 2 nên số cần tìm nằm ở phía bên phải của mid:
Lúc này L = mid + 1 đã lớn hơn R, nên ta suy ra target không nằm trong nums và trả về kết quả -1.
5. Code bằng máy
Code của chúng ta sẽ như sau:
public int search(int[] nums, int target) {
return bSearch(nums, 0, nums.length - 1, target);
}
public int bSearch(int[] a, int L, int R, int target){
if(L > R) {
return -1;
}
int mid = (L + R)/2;
if (a[mid] == target) {
return mid;
}
else if (a[mid] < target){
return bSearch(a, mid + 1, R, target);
}
return bSearch(a, L, mid - 1, target);
}
6. Kết thúc
Qua bài viết này, mình đã chia sẻ cho các bạn cách mình tư duy khi giải bài tập trên leetcode. Hi vọng bài viết giúp ích cho các bạn trong cách tư duy để giải các bài tập khác. Xin cám ơn các bạn đã dành thời gian đọc và theo dõi. Peace!!!

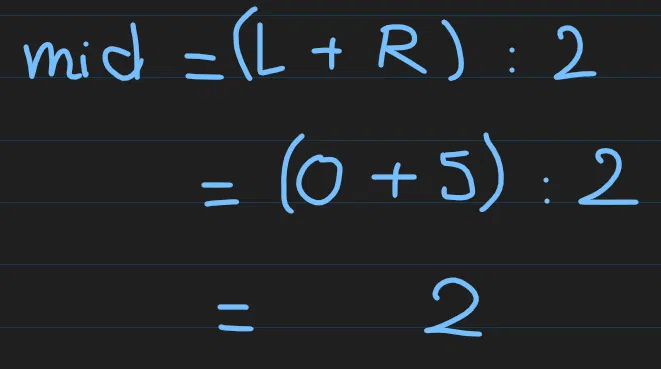
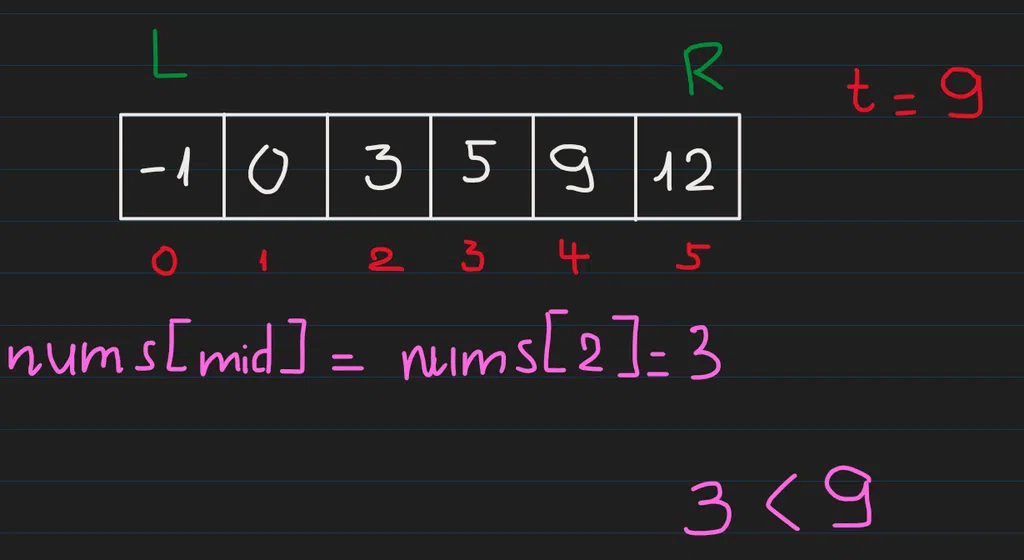
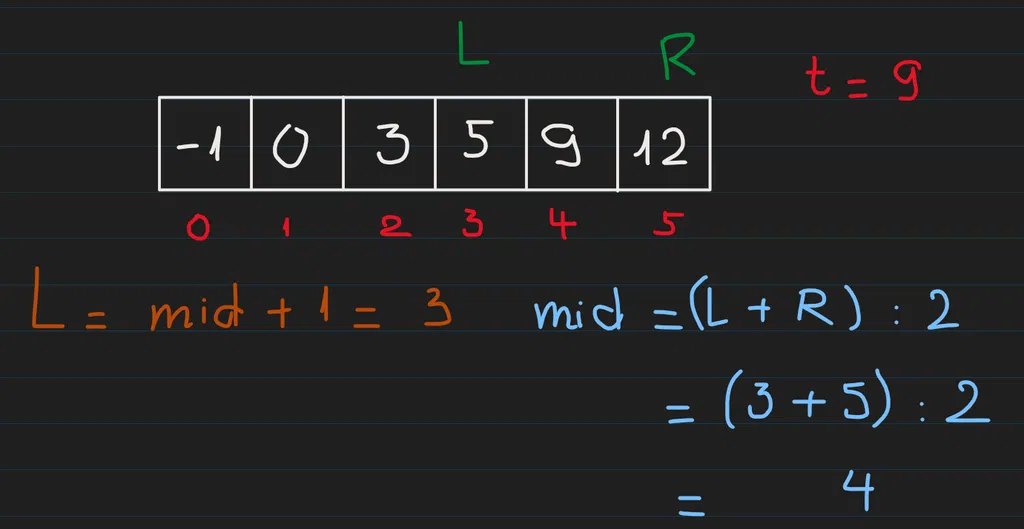
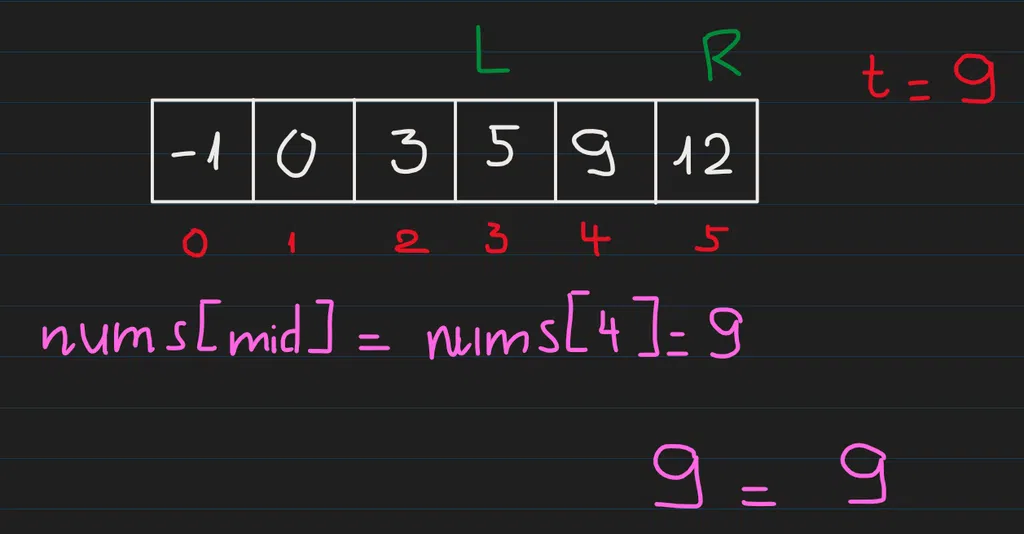
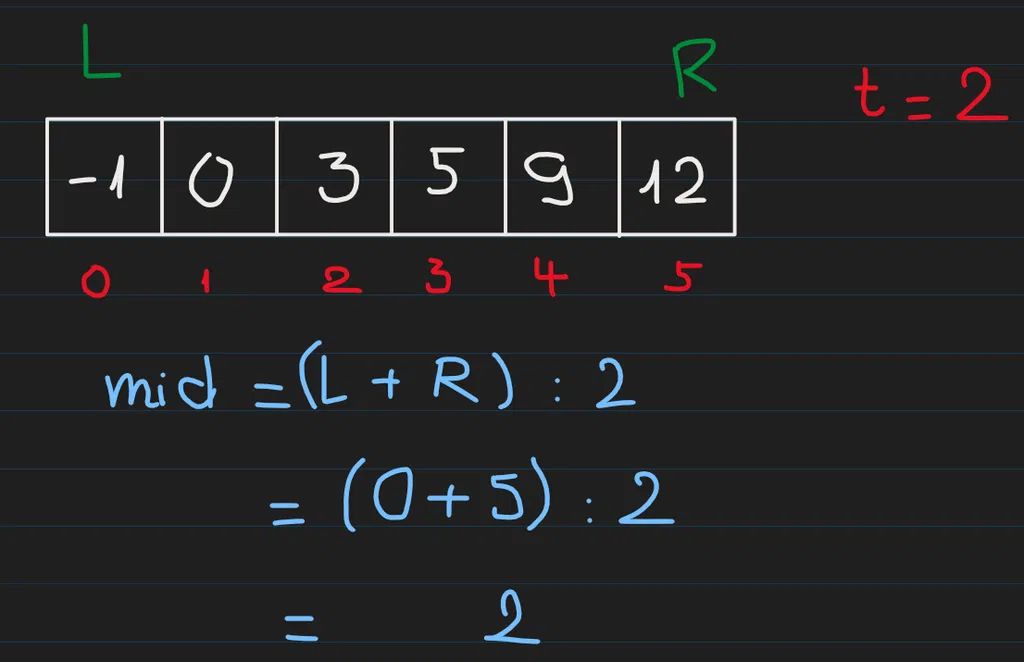
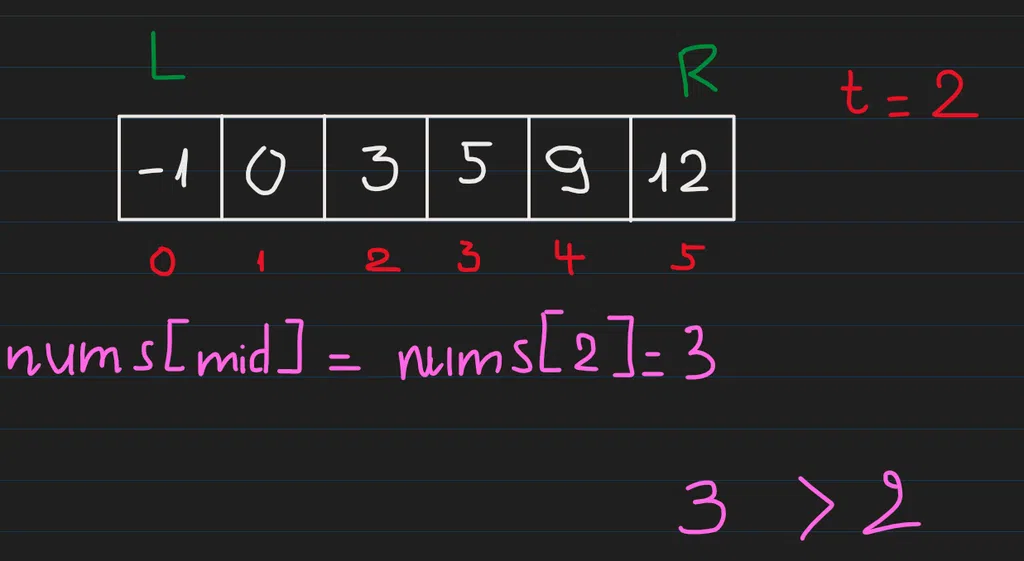
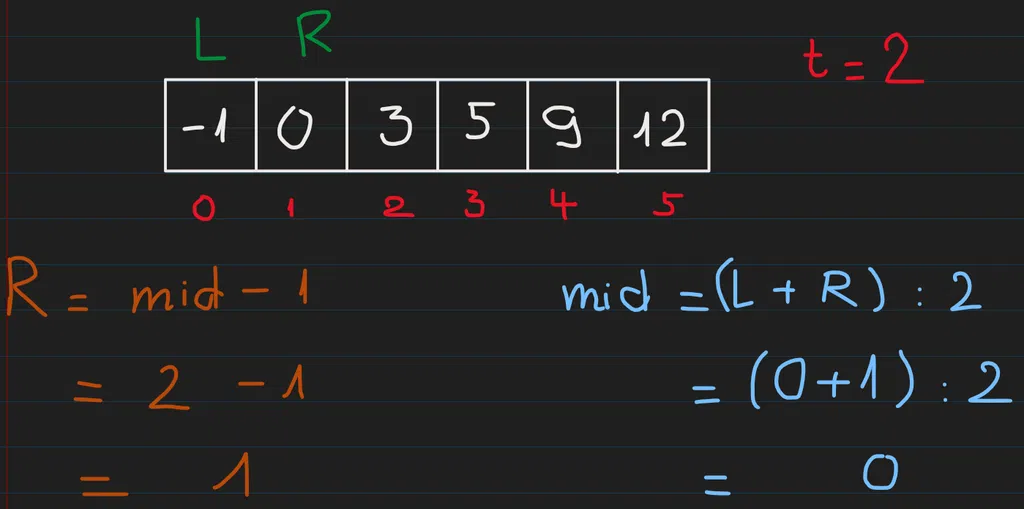

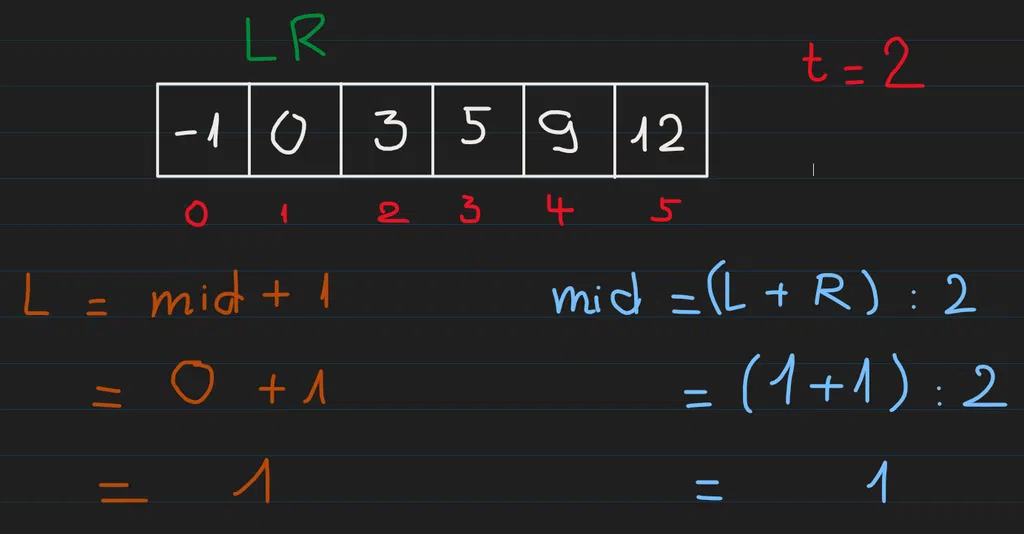
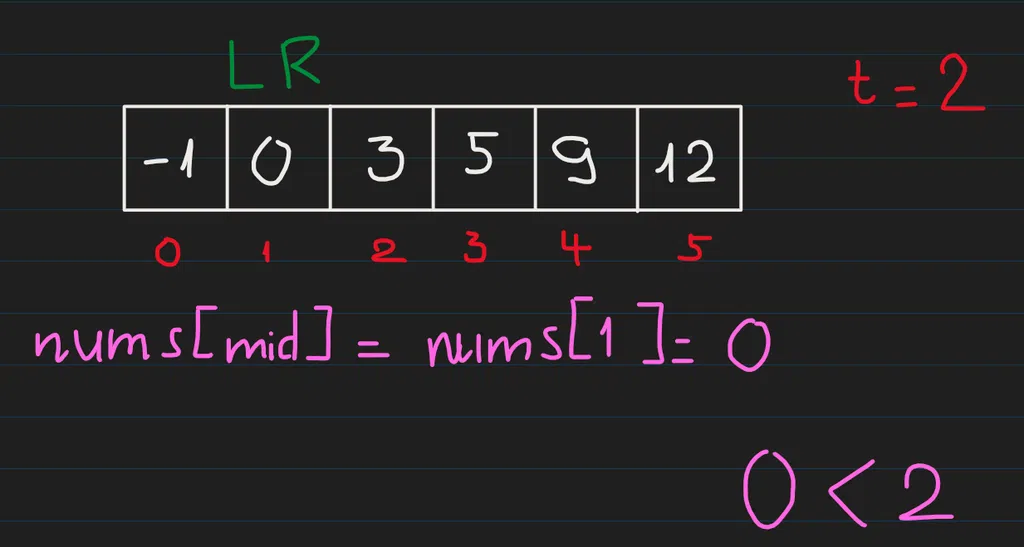
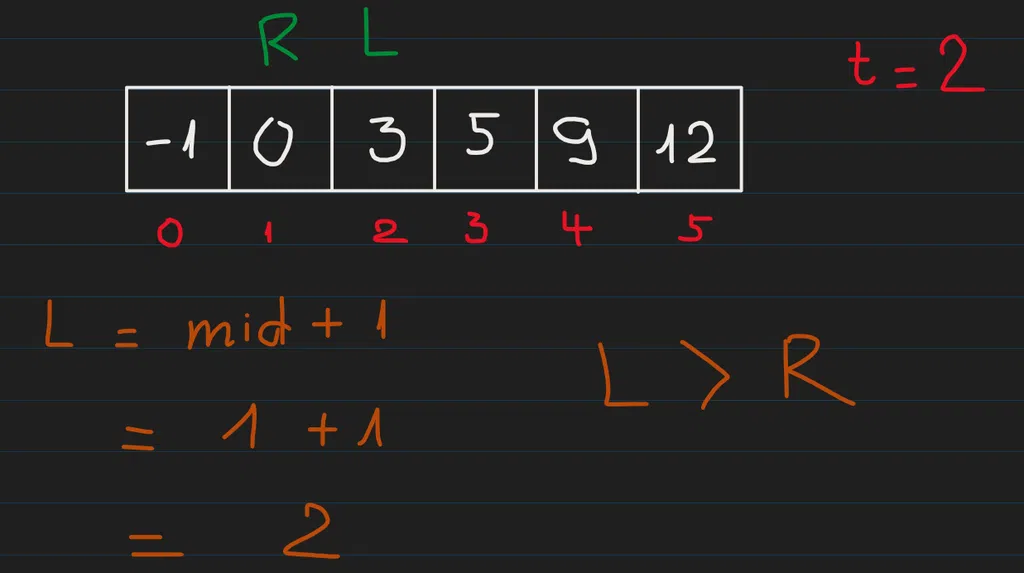
Bình luận