Tác giả: Lê Trung Kiên lớp java 08
Email: lekien.2803.cg@gmail.com
SĐT: 0942096947
Link bài toán: https://leetcode.com/problems/difference-between-element-sum-and-digit-sum-of-an-array/
1.Mở đầu
Xin chào các bạn, mình viết ra bài viết này để chia sẻ phương pháp giải cũng như tư duy của mình về bài toán này của leetcode. Phương pháp của mình có thể không phải là tối ưu nhất, tuy nhiên mình sẽ phân tích, chia nhỏ bài toán ra thành các module nhỏ hơn để dễ giải quyết cũng như giúp các bạn hiểu được các yêu cầu mà bài toán đưa ra.
2. Đề bài
Cho bạn một mảng số nguyên dương nums.
- Tính tổng các phần tử có trong mảng
nums. - Tính tổng các chữ số (kể cả trùng lặp) có trong mảng
nums.
Trả về kết quả là hiệu tuyệt đối giữa tổng các phần tử và tổng các chữ số của mảng nums.
Điều kiện đề bài:
1 <= nums.length <= 20001 <= nums[i] <= 2000
Bài toán minh họa 1:
Input: nums = [1,15,6,3]
Output: 9
Explanation:
The element sum of nums is 1 + 15 + 6 + 3 = 25.
The digit sum of nums is 1 + 1 + 5 + 6 + 3 = 16.
The absolute difference between the element sum and digit sum is |25 - 16| = 9.
Bài toán minh họa 2:
Input: nums = [1,2,3,4]
Output: 0
Explanation:
The element sum of nums is 1 + 2 + 3 + 4 = 10.
The digit sum of nums is 1 + 2 + 3 + 4 = 10.
The absolute difference between the element sum and digit sum is |10 - 10| = 0.
3. Phân tích
Đề bài này cũng không có gì quá phức tạp, chúng ta chỉ cần làm ba công việc chính:
- Tính tổng các phần tử trong mảng.
- Tính tổng các chữ số xuất hiện trong mảng.
- Tính hiệu tuyệt đối giữa tổng các phần tử và tổng các chữ số.
Thế là xong!
4. Đến giờ code thôi
Trước hết chúng ta hãy chạy code bằng cơm đã nhé:
Đầu tiên ta cần hai biến chứa kết quả của tổng các phần tử và tổng các chữ số:
int eleSum = 0,
digSum = 0;
Tiếp theo chúng ta sẽ tính tổng các phần tử trong mảng, cái này quá dễ rồi, chỉ cần làm một vòng lặp for, cộng các phần tử lại với nhau là xong:
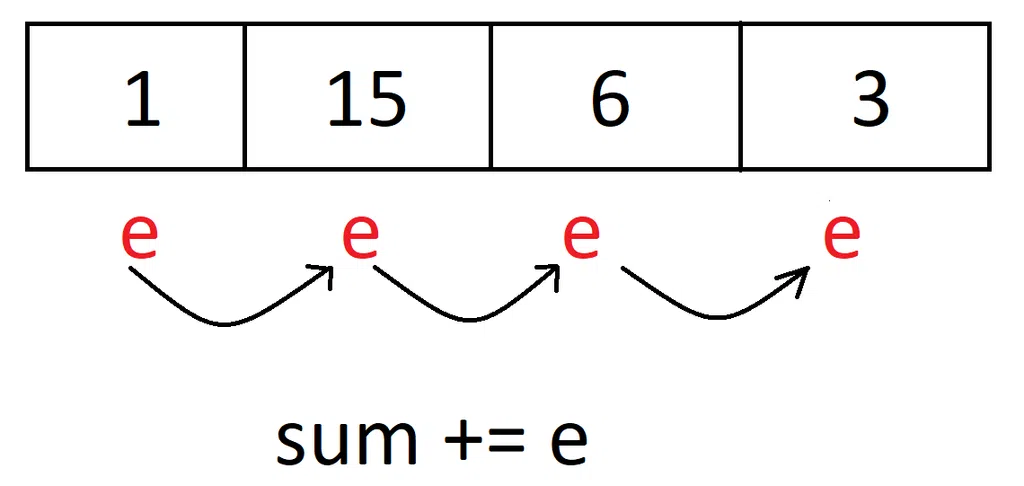
for (int e : nums) {
eleSum += e;
}
Rồi bây giờ cần tìm tổng các chữ số trong mảng. Nhưng mà làm thế nào để lấy ra được từng chữ số của một số nhỉ?
Có cách rồi, ta sẽ đổi từ kiểu int sang String để lấy từng chữ số, ví dụ nhé:
int i = 15;
String numString = String.valueOf(i); \\ số 15 giờ sẽ thành "15"
numString.charAt(0); \\ kết quả là '1' - kiểu char
numString.charAt(1); \\ kết quả là '5' - kiểu char
Nhưng kết quả ta cần là dạng int cơ mà, bây giờ đang là char rồi còn đâu. Đừng lo, chỉ cần lấy char trừ đi ‘0’ là sẽ về kiểu int ngay. Vậy nên ta có code như sau:
for (int e : nums) {
eleSum += e;
String numString = String.valueOf(e);
for (int i = 0; i < numString.length(); i++) {
digSum += numString.charAt(i) - '0';
}
}
Và cuối cùng ta tính hiệu tuyệt đối nữa là xong:
int res = Math.abs(eleSum - digSum);
Tổng kết lại ta có:
public int differenceOfSum(int[] nums) {
int eleSum = 0,
digSum = 0;
for (int e : nums) {
eleSum += e;
String numString = String.valueOf(e);
for (int i = 0; i < numString.length(); i++) {
digSum += numString.charAt(i) - '0';
}
}
int res = Math.abs(eleSum - digSum);
return res;
}
Ok vậy là kết quả đúng, chạy bằng cơm như thế cái đã. Nhưng có một vấn đề rất là to, ấy là độ phức tạp của bài toán đang là O(n^2), và nếu các bạn để ý điều kiện đề bài, số phần tử trong mảng có thể lên đến 2000, mỗi phần tử trong mảng có giá trị lên đến 2000 luôn. Trong trường hợp tệ nhất, 2000 phần tử, số nào số nấy cũng toàn 4 chữ số thì ối giời ơi với hai cái vòng lặp lồng nhau như thế kia.
Không ổn, như trên chỉ là code chạy bằng cơm thôi, chúng ta phải cải thiện code hơn nữa!
Vấn đề nâng độ phức tạp của bài toàn lên chính là việc chúng ta phải thêm vòng lặp chỉ để lấy từng chữ số trong mảng. Vậy có cách nào khác không?
Tất nhiên là có rồi, ta sẽ sử dụng phép chia (/) và phép chia lấy dư (%) để giải quyết bài toán này. Theo điều kiện đề bài, ta có 1 <= nums[i] <= 2000, nghĩa là mỗi phần tử sẽ có giá trị lên đến 2000, không quá bốn chữ số và có thể chia hết cho 1000. Ok vậy ta làm như sau:
Ví dụ với số 1357:
int i = 1357;
i / 1000 = 1 // ta lấy được số hàng nghìn
i / 100 % 10 = 3 // lấy i/100 thì kết quả ra 13, nhưng ta cần số hàng trăm là 3 thôi, vậy thì phải thêm phép chia lấy dư %
i / 10 % 10 = 5 // lấy i/10 thì được 135, ta cần số hàng chục nên sẽ dùng phép chia lấy dư %
i % 10 = 7 // và cuối cùng là lấy số hàng đơn vị thì ta chỉ cần làm phép chia lấy dư với 10 là được.
Đã xong phần lấy chữ số, giờ đến phần cộng tổng. Như bài toán minh họa số 2, ta có thể viết như sau cho dễ hình dung:|1 + 2 + 3 + 4 - (1 + 2 + 3 + 4)| = |1 + 2 + 3 + 4 - 1 - 2 - 3 - 4|
Các bạn có thấy nó hơi rườm rà không? Cộng vào rồi lại trừ đi, sao ta không lấy phần tử trừ đi chính các chữ số của nó ngay từ đầu nhỉ?|(1 - 1) + (2 - 2) + (3 - 3) + (4 - 4)|
Ô kê vậy thì ta sẽ viết lại như sau:
public int differenceOfSum(int[] nums) {
int res = 0;
for (int i : nums) {
res += i - (i/1000 + i/100%10 + i/10%10 + i%10);
}
return Math.abs(res);
}
Quào! Ô kìa, độ phức tạp bài toán về O(n) rồi! Quá ngon!
5. Kết thúc
Qua bài viết này, mình đã chia sẻ cho các bạn cách mình tư duy khi giải bài tập trên leetcode. Hi vọng bài viết giúp ích cho các bạn trong cách tư duy để giải các bài tập khác. Xin cám ơn các bạn đã dành thời gian đọc và theo dõi.


Bình luận