Nếu bạn đang có ý định trở thành một Data Scientist (nhà khoa học dữ liệu) thì hiện tại đang là 1 thời điểm không hề tồi chút nào. Những con người kể cả khó tính nhất cũng sẽ đổ dồn sự chú ý khi bạn đề cập tới Big Data trong cuộc hội thoại, đám đông sẽ cảm thấy hào hứng khi được nghe bạn chém gió về Trí tuệ nhân tạo cũng như Học máy. Thậm chí những con số do Google cung cấp tại đây còn cho thấy: tất cả vẫn chưa có dấu hiệu dừng lại, chúng vẫn tiếp tục phát triển với tốc độ rất nhanh.
Càng ngày càng có rất nhiều các giải thuật 'thông minh' đã được phát minh ra để giúp đỡ các nhà khoa học dữ liệu. Tất cả chúng nhìn chung đều có vẻ rất phức tạp, nhưng nếu chúng ta hiểu được và biết cách phối hợp một cách nhuần nhuyễn thì mọi việc sẽ trở nên dễ dàng hơn rất nhiều.

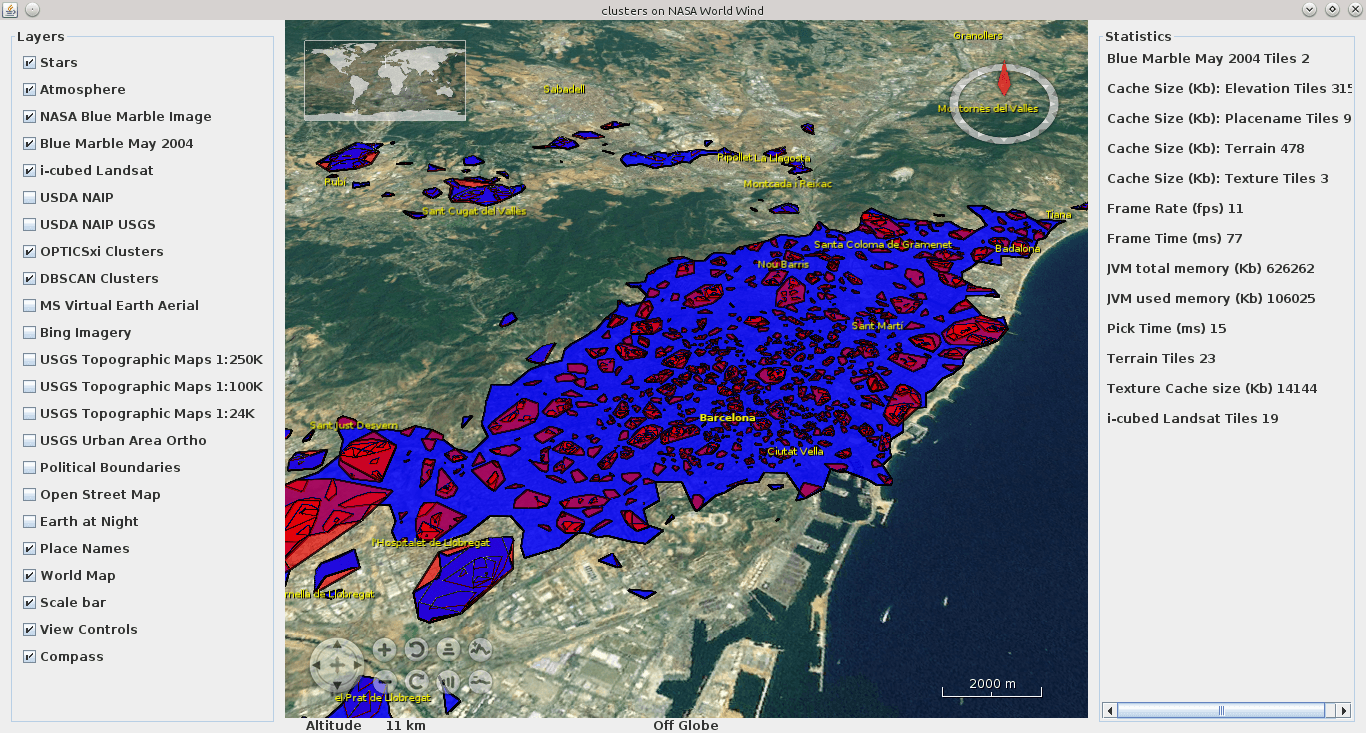
Các khóa học về khai phá dữ liệu (Data Mining) hoặc học máy (Machine Learning) vẫn thường mở đầu bằng những ví dụ về phân cụm, lí do đơn giản bởi vì chúng rất thực tế và không quá khó hiểu. Bài toán phân cụm là 1 nhánh ứng dụng chính của lĩnh vực Unsupervised Learning (Học không giám sát), trong đó dữ liệu được mô tả trong bài toán không được dán nhãn (tức là không có đầu ra). Trong trường hợp này, thuật toán sẽ tìm cách phân cụm - chia dữ liệu thành từng nhóm có đặc điểm tương tự nhau, nhưng đồng thời đặc tính giữa các nhóm đó lại phải càng khác biệt càng tốt.
Dữ liệu của chúng ta có thể là bất cứ thứ gì, chẳng hạn như dữ liệu về khách hàng: Thuật toán phân cụm sẽ rất hữu ích trong việc đánh giá và chia thành các nhóm người dùng khác nhau, rồi từ đó ta có thể đưa ra những chiến lược marketing phù hợp trên từng nhóm người dùng đó.
K-Means Clustering
Sau khi dạo qua những màn giới thiệu chung, đa số các khóa học Data Mining sẽ bắt đầu luôn với K-Means: 1 thuật toán tuy đơn giản nhưng lại khá hiệu quả và được sử dụng rộng khắp. Trước khi bắt tay vào làm, chúng ta cần phải xác định sẵn 2 thứ: đó là hàm khoảng cách được sử dụng (ví dụ như khoảng cách Euclid) và số lượng nhóm mong muốn (ta sẽ kí hiệu trong bài viết này là k)
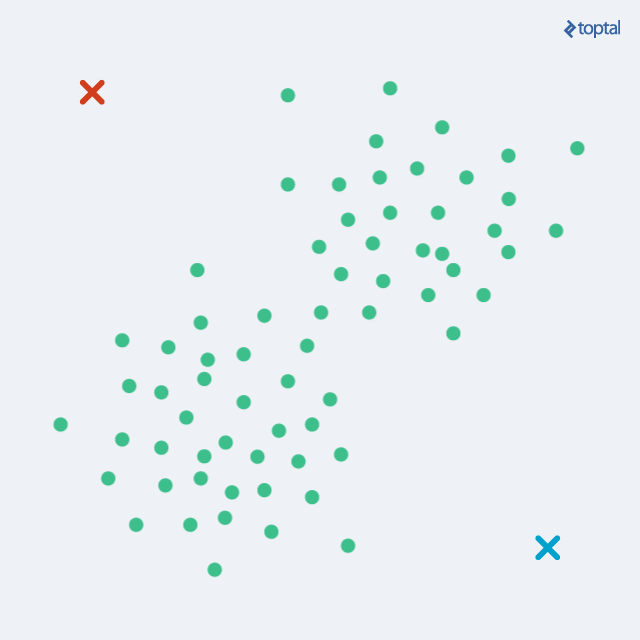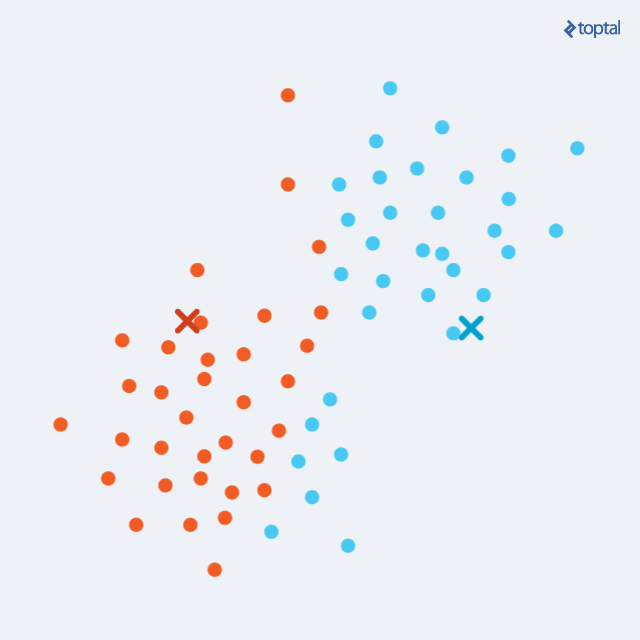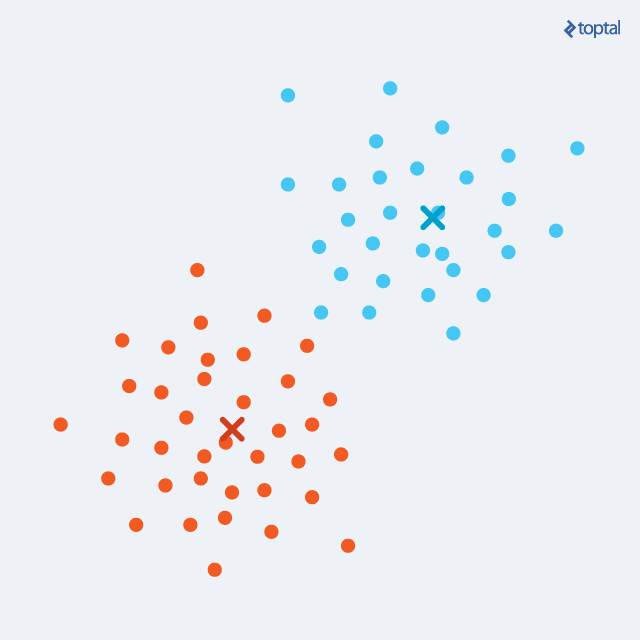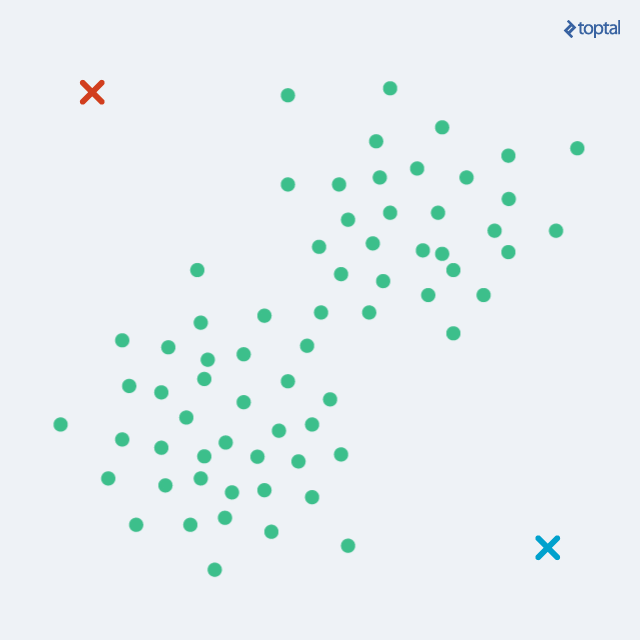
Thuật toán bắt đầu với việc chọn ra tâm của từng cụm. Chúng ta có thể đơn giản chọn k điểm ngẫu nhiên trong bộ, hoặc sử dụng một số hướng tiếp cận nào khác, nhưng nhìn chung ngẫu nhiên vẫn là cách tốt nhất. Rồi kế tiếp, luân phiên lặp lại 2 giai đoạn sau:
- Giai đoạn gán: gán từng phần tử trong bộ dữ liệu của chúng ta vào các cụm. Cách thức tiến hành đó là: với mỗi điểm, hãy tính khoảng cách từ điểm đó tới vị trí các tâm, sau cùng: tâm nào gần nhất thì gán vào cụm ứng với cái tâm đó
- Giai đoạn cập nhật: duyệt từng cụm, cập nhật lại tọa độ của tâm: Như đã biết, sau giai đoạn 1, chúng ta đã thu được k cụm ứng với dãy các điểm được gán cho từng cụm. Tọa độ tâm mới của cụm sẽ bằng trung bình cộng tọa độ các điểm trong cụm
Sau càng nhiều vòng lặp, các tâm càng di chuyển chậm dần, và tổng khoảng cách từ mỗi điểm trong cụm tới tâm cụm lại càng nhỏ đi. Quá trình sẽ kết thúc cho tới khi hàm tổng khoảng cách hội tụ (tức là không có sự thay đổi nào xảy ra ở giai đoạn gán nữa). Lúc này tọa độ tâm vẫn sẽ bằng trung bình cộng các điểm hiện tại trong cụm, hay nói cách khác tâm sẽ không còn di chuyển tiếp nữa. Chú ý thuật toán K-Means chỉ đảm bảo được quá trình này sẽ đưa hàm tổng khoảng cách hội tụ tới điểm cực tiểu địa phương, chứ không chắc chắn đó là giá trị nhỏ nhất của toàn bộ hàm số. Tuy nhiên, điều này là có thể chấp nhận được vì KHÔNG phải mô hình nào càng sát với bộ dữ liệu huấn luyện thì cũng sẽ càng tốt.
Ta có thể nhận thấy rằng việc lựa chọn tâm lúc khởi điểm cũng có ảnh hưởng tới kết quả cuối cùng thu được, do đó đã nảy sinh rất nhiều ý kiến trái chiều về vấn đề này. Một ý tưởng đơn giản là cho chạy K-Means nhiều lần với mỗi bộ tâm ngẫu nhiên khác nhau, rồi sau đó chọn ra mô hình tốt nhất thông qua việc xét giá trị nhỏ nhất của các hàm tổng khoảng cách ứng với chúng.
Một hướng tiếp cận khác trong việc chọn tâm ban đầu đó là chọn những điểm "xa nhất". Việc này có thể cho kết quả tốt hơn, tuy nhiên ta sẽ mắc phải vấn đề với những phần tử "nhiễu", đó là những phần tử nằm riêng lẻ một mình tách biệt với phần còn lại trong bộ dữ liệu. Do đó chúng sẽ tự lập ra 1 cụm riêng của chính mình.
Có một cách giải quyết đã được phát minh để cân bằng đồng thời được cả 2 điều trên, nó có tên gọi là K-Means++: trong đó, tâm khởi đầu vẫn được chọn ngẫu nhiên, nhưng là chọn lần lượt (thay vì đồng loạt) và kèm theo xác suất ngẫu nhiên tỉ lệ thuận với khoảng cách tới điểm tâm vừa chọn trước đó. Tức là, các điểm càng nằm phía xa sẽ có khả năng được chọn làm tâm kế tiếp càng lớn. Do đó, nếu có 1 nhóm các điểm, khả năng chỉ 1 điểm từ nhóm đó được chọn làm tâm cũng sẽ cao hơn.
K-Means++ cũng đang được chọn sử dụng cho bước khởi tạo của thuật toán K-Mean trong thư viện Scikit-learn của Python. Nếu bạn đang lập trình Python, bạn có thể dùng ngay thư viện này. Đối với Java, thư viện Weka sẽ là 1 sự lựa chọn đáng để cân nhắc.
Java (Weka)
// Load some data
Instances data = DataSource.read("data.arff");
// Create the model
SimpleKMeans kMeans = new SimpleKMeans();
// We want three clusters
kMeans.setNumClusters(3);
// Run K-Means
kMeans.buildClusterer(data);
// Print the centroids
Instances centroids = kMeans.getClusterCentroids();
for (Instance centroid: centroids) {
System.out.println(centroid);
}
// Print cluster membership for each instance
for (Instance point: data) {
System.out.println(point + " is in cluster " + kMeans.clusterInstance(point));
}Python (Scikit-learn)
>>> from sklearn import cluster, datasets
>>> iris = datasets.load_iris()
>>> X_iris = iris.data
>>> y_iris = iris.target
>>> k_means = cluster.KMeans(n_clusters=3)
>>> k_means.fit(X_iris)
KMeans(copy_x=True, init='k-means++', ...
>>> print(k_means.labels_[::10])
[1 1 1 1 1 0 0 0 0 0 2 2 2 2 2]
>>> print(y_iris[::10])
[0 0 0 0 0 1 1 1 1 1 2 2 2 2 2]Ở trong ví dụ Python phía trên, ta sử dụng bộ dữ liệu Iris chứa kích thước đài hoa và cánh hoa cho 3 giống hoa Iris khác nhau, chia những dữ liệu này thành 3 cụm, rồi sau đó so sánh với giá trị thực tế của chúng, để kiểm tra độ chính xác của thuật toán.
Trong trường hợp này, chúng ta thấy rằng dữ liệu được tách thành 3 cụm (ứng với 3 giống hoa) khác nhau và K-Means đã nhận ra chính xác những phần tử nào cùng nằm chung 1 cụm (Chú ý rằng Unsupervised Learning là bài toán không có nhãn nên chỉ số k bằng (0, 1, 2) ở trên chỉ là ngẫu nhiên, có tác dụng phân biệt chứ không phải là nhãn đầu ra).
Tuy nhiên, làm cách nào mà ta chọn ra được số cụm (k) thích hợp? Câu hỏi tương tự như vậy thường rất phổ biến trong Học máy. Nếu chúng ta yêu cầu nhiều cụm hơn, dữ liệu sẽ được chia nhỏ ra, và giá trị error (tổng khoảng cách) cũng sẽ nhỏ hơn. Vậy, như thế có phải sẽ là tốt hơn nếu như ta chọn k lớn nhất có thể? Chúng ta có thể chọn k = m (số điểm), như thế mỗi điểm sẽ trở thành tâm của chính nó và mỗi cụm sẽ chỉ có 1 điểm? Điều đó không sai, error sẽ bằng 0, nhưng chúng ta sẽ không thể tìm được mô tả đơn giản cho dữ liệu, và mô hình thu được cũng không thể phủ được những điểm mới thêm vào. Vấn đề này có tên gọi là overfitting, và tất nhiên chúng ta sẽ không mong gặp phải nó.
Một cách để giải quyết vấn đề này là bổ sung thêm hàm phạt (penalty) cho số lượng cụm. Từ đó, mục tiêu của ta lúc này không chỉ còn giảm thiểu error, mà phải cân bằng cả error + penalty. Giá trị error sẽ tiến dần tới 0 khi chúng ta tăng số lượng cụm, nhưng đồng thời penalty cũng tăng theo. Quá trình tăng số lượng cụm sẽ dừng lại khi mà lượng error giảm đi thấp hơn so với giá trị penalty, và kết quả thu được là kết quả tối ưu. Có một giải pháp sử dụng Bayesian Information Criterion (BIC) để tính k có tên gọi là X-Means [Pelleg and Moore, 2000].
Một thứ khác chúng ta cần quan tâm đó là hàm khoảng cách. Hiển nhiên, với những điểm nằm trong không gian, khoảng cách Euclid rõ ràng là hiệu quả nhất, nhưng đôi khi ta cần thêm vài "mánh khóe" cho những loại dữ liệu đặc trưng khác nhau, ví dụ như các giá trị rời rạc,... Việc này yêu cầu khá nhiều kiến thức chuyên ngành liên quan tới dữ liệu đó. Hoặc, chúng ta có thể nhờ tới sự trợ giúp của Học máy để huấn luyện ra hàm khoảng cách thích hợp nhất. Nếu bạn có 1 tập các dữ liệu huấn luyện (đã biết trước chúng được phân cụm thế nào qua nhãn của chúng), kĩ thuật Supervised Learning (học có giám sát) có thể được ứng dụng để tìm ra hàm khoảng cách thích hợp, rồi áp dụng nó vào trong dữ liệu cần phân cụm.
Ngoài ra, có 1 thuật toán phân cụm khác có tên là Expectation-Maximization (EM) cũng gần tương tự với 2 giai đoạn được dùng trong K-Means. Nói chính xác thì K-Means có thể coi là 1 phiên bản đơn giản hơn của EM. Tuy nhiên, đừng nhầm lẫn chúng với nhau mặc dù có rất nhiều điểm chung giữa 2 thuật toán này.
EM Clustering
Như vậy, với K-Means: mỗi điểm sẽ được gán cho 1 nhóm và mỗi nhóm được đại diện bởi 1 tâm. Điều này không quá phức tạp, vì chúng ta chưa gặp phải vấn đề cụm chồng chéo, hoặc những cụm có hình dạng khác hình tròn. Với EM, ta bây giờ có thể tiến một bước xa hơn nữa và đặc tả mỗi cụm bằng tâm của nó (kì vọng), covariance (hiệp phương sai - qua đó ta có thể biểu diễn được cụm hình elip) và weight (kích thước của cụm). Xác suất mà 1 điểm thuộc về 1 cụm bây giờ được tính bằng xác suất phân phối Gauss đa biến.

Chúng ta sẽ bắt đầu EM bằng cách tính, với mỗi điểm, xác suất mà nó thuộc về từng cụm là bao nhiêu (tất nhiên, các cụm ban đầu cũng được khởi tạo ngẫu nhiên). Đây là bước E-step. Nếu 1 cụm là "ứng viên" tốt đối với 1 điểm, nó sẽ có xác suất gần với 1. Tuy nhiên, có xảy ra trường hợp 2 hay nhiều cụm cùng là ứng viên tốt, do đó điểm của chúng ta lúc này sẽ có phân phối xác suất giữa các cụm. Tính chất này của thuật toán được gọi là "soft clustering".
Bước M-step bây giờ tính toán lại các tham số của mỗi cụm, bằng cách sử dụng kết quả xác suất của các điểm được tính ở bước E-step. Để tính toán tâm mới, covariance mới và weight mới của 1 cụm, mỗi dữ liệu điểm sẽ được đánh trọng số tỉ lệ thuận với xác suất biến cố "điểm đó thuộc cụm" (lấy từ E-step).
Luân phiên 2 bước này sẽ làm tăng giá trị log-likelihood của hàm xác suất cho tới khi giá trị này hội tụ tới cực đại. Nói thêm, tương tự với K-Means, thuật toán EM chỉ cho ta giá trị cực đại địa phương, vì vậy ta có thể sẽ cần phải thực hiện thuật toán nhiều lần để tìm được mô hình tốt hơn nữa.
Nếu ta muốn đưa ra quyết định 1 điểm bất kỳ thuộc cụm nào, đơn giản chỉ cần chọn cụm cho ta giá trị xác suất cao nhất ứng với điểm đó. Và ta cũng có thể hoàn toàn tái tạo lại được 1 mẫu tương tự như dữ liệu ban đầu từ mô hình dựa vào dãy các xác suất thu được.
Bài viết gốc: https://www.toptal.com/machine-learning/clustering-algorithms

Bình luận